Реферат: Системи випадкових величин
![]() , (1.2)
, (1.2)
яка визначає ймовірність того, що випадкова величина X приймає значення менше ніж x , а ![]() - менше ніж y . Геометрична інтерпретація інтегральної функції сумісного розподілу полягає в тому, що вона визначає ймовірність попадання випадкової точки
- менше ніж y . Геометрична інтерпретація інтегральної функції сумісного розподілу полягає в тому, що вона визначає ймовірність попадання випадкової точки ![]() у нескінченний заштрихований квадрат із вершиною в точці
у нескінченний заштрихований квадрат із вершиною в точці ![]() (рис 1.1).
(рис 1.1).
Інтегральна функція розподілу випадкового вектора ![]() має такі очевидні властивості.
має такі очевидні властивості.
Властивість 1 .
![]() .
.
Властивість 2 .Функція ![]() неспадна по кожному аргументу
неспадна по кожному аргументу
![]() , якщо
, якщо ![]() ;
;
![]() , якщо
, якщо ![]() .
.
Властивість 3 .Мають місце граничні співвідношення
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Властивість Для функція ![]() мають місце ще і такі граничні співвідношення
мають місце ще і такі граничні співвідношення
![]() ,
,
![]() ,
,
![]() - інтегральна функція розподілу компоненти X випадкового вектора
- інтегральна функція розподілу компоненти X випадкового вектора ![]() .
.
![]() - інтегральна функції розподілу компоненти Y випадкового вектора
- інтегральна функції розподілу компоненти Y випадкового вектора ![]() .
.
З використанням функції розподілу (1.2) легко можна обчислити ймовірність попадання випадкової точки у напівсмугу ![]() та
та ![]() (рис 1.2)
(рис 1.2)
![]() , (1.3а)
, (1.3а)
![]() .(1.3б)
.(1.3б)
Імовірність попадання випадкової точки у напівсмугу дорівнює приросту інтегральної функції сумісного розподілу по відповідному аргументу.
Доведення. Імовірність попадання у напівсмугу ![]() дорівнює різниці ймовірності попадання точки у нескінченний квадрат з вершиною
дорівнює різниці ймовірності попадання точки у нескінченний квадрат з вершиною ![]() (
(![]() )і ймовірності попадання точки у нескінченний квадрат з вершиною
)і ймовірності попадання точки у нескінченний квадрат з вершиною ![]() (
(![]() . Звідси і слідує рівність (1.3а)
. Звідси і слідує рівність (1.3а)
Імовірність попадання випадкової точки у прямокутник утворений прямими
![]()
(рис.1.3) обчислюється за формулою
![]() (1.4)
(1.4)
Доведення. Імовірність попадання у прямокутник дорівнює різниці ймовірності попадання точки у напівсмугу ![]() (
(![]() )і ймовірності попадання у напівсмугу
)і ймовірності попадання у напівсмугу ![]() (
(![]() ). Звідси і слідує рівність (1.3а)
). Звідси і слідує рівність (1.3а)
Приклад 1.2. Знайти ймовірність пападання випадкової точки ![]() у прямокутник обмеженний прямими
у прямокутник обмеженний прямими ![]() ,
, ![]() ,
, ![]() ,
, ![]() , якщо відома інтегральна функція сумісного розподілу
, якщо відома інтегральна функція сумісного розподілу
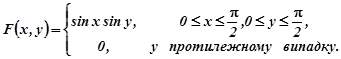
Розв’язування . За формулою (1.4) в якій ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]()