Реферат: Системи випадкових величин

Система двох неперервних випадкових величин однозначно визначається густиною сумісного розподілу ймовірностей

. (1.5)

Приклад 1.3. Знайти густину сумісного розподілу системи випадкових величин, якщо відома інтегральна функція сумісного розподілу

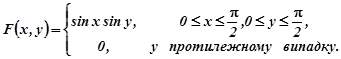
Розв’язування . За формулою (1.5)

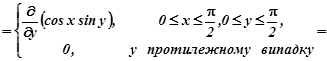
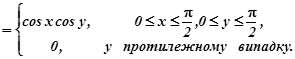
Інтегральна функція сумісного розподілу неспадна по кожному аргументу і тому

.

За відомою густиною сумісного розподілу інтегральну функцію сумісного розподілу можна визначити за формулою

(1.6)

Приклад 1. Знайти інтегральну функцію сумісного розподілу системи випадкових величин, якщо відома густина сумісного розподілу

.

Розв’язування . За формулою (1.6)

.

Враховуючи , що (властивість 3), для густини сумісного розподілу можна записати рівність нормування

.

Ймовірність попадання випадкової точки у довільну область (рис.1.3) обчислюється за формулою

,(1.7)

яка одразу слідує з означення подвійного інтеграла

Приклад 1.5. Система випадкових величин задана густиною сумісного розподілу

.

Знайти ймовірність попадання випадкової точки у прямокутник з вершинами , ,,.

Розв’язування . За формулою (1.7)

.