Реферат: Системи випадкових величин

З рівностей (3.4) та (3.6) слідує, що обидві прямі проходять через точку . Цю точку називають центром сумісного розподілу двовимірної випадкової величини .

Лінійна кореляція нормальних величин

Якщо обидві функції регресій X на Y та Y на X є лінійними функціями, то говорять, що X та Y зв’язані лінійною кореляційною залежністю. Графіки лінійних регресій – прямі лінії, які співпадають з прямими середньоквадратичних регресій.

Якщо двовимірна випадкова величина (X ,Y ) має нормальний закон розподілу у сукупності, то X та Y зв’язані лінійною кореляційною залежністю.

Доведення .Для спрощення густину нормального сумісного розподілу можна записати у вигляді

,

, , , .

Для знаходження регресії необхідно знайти розподіл компоненти :

,

.

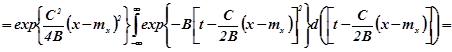
З врахуванням цього

.

,

,

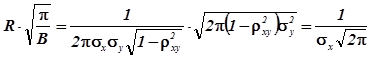Тому

.

Густина умовного розподілу компоненти

.

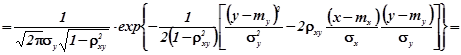
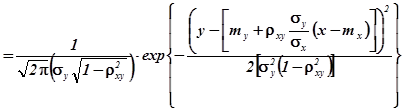Порівнюючи одержану густину умовного розподілу з густиною нормального розподілу можна зробити висновок, що умовний розподіл компоненти є нормальним з математичним сподіванням (функцією регресії на )

та умовною дисперсією