Реферат: Теоретическая физика: механика

Преподаватель Джежеря Ю.И. ___________

Методист ____________________

План-конспект занятия

По теоретической физике

Студента V курса физико-математического факультета, гр. ОФ-61

Филатова Александра Сергеевича

Дата проведения занятия: 20.12.2000

Тема: «Канонические преобразования. Функция Гамильтона-Якоби. Разделение переменных»

Цели: Развить навык использования канонических преобразований. Закрепить умение осуществлять преобразования Лежандра для перехода к производящей функции от необходимых переменных. Научить использовать метод Гамильтона-Якоби при решении задач с разделением переменных. Сформировать понимание сути и могущественности метода. Воспитывать трудолюбие, прилежность.

Тип занятия: практическое.

Ход занятия

Краткие теоретические сведения

Канонические преобразования

Канонические преобразования переменных – это такие преобразования, при которых сохраняется канонический вид уравнений Гамильтона. Преобразования производят с помощью производящей функции, которая является функцией координат, импульсов и времени. Полный дифференциал производящей функции определяется следующим образом:

Выбирая производящую функцию от тех или иных переменных, получаем соответствующий вид канонических преобразований. Заметим, что если частная производная будет браться по "малым" , то будем получать малое , если же по "большим" , то и получать будем соответственно .

Функция Гамильтона-Якоби

При рассмотрении действия, как функции координат (и времени), следует выражение для импульса:

Из представления полной производной действия по времени следует уравнение Гамильтона-Якоби:

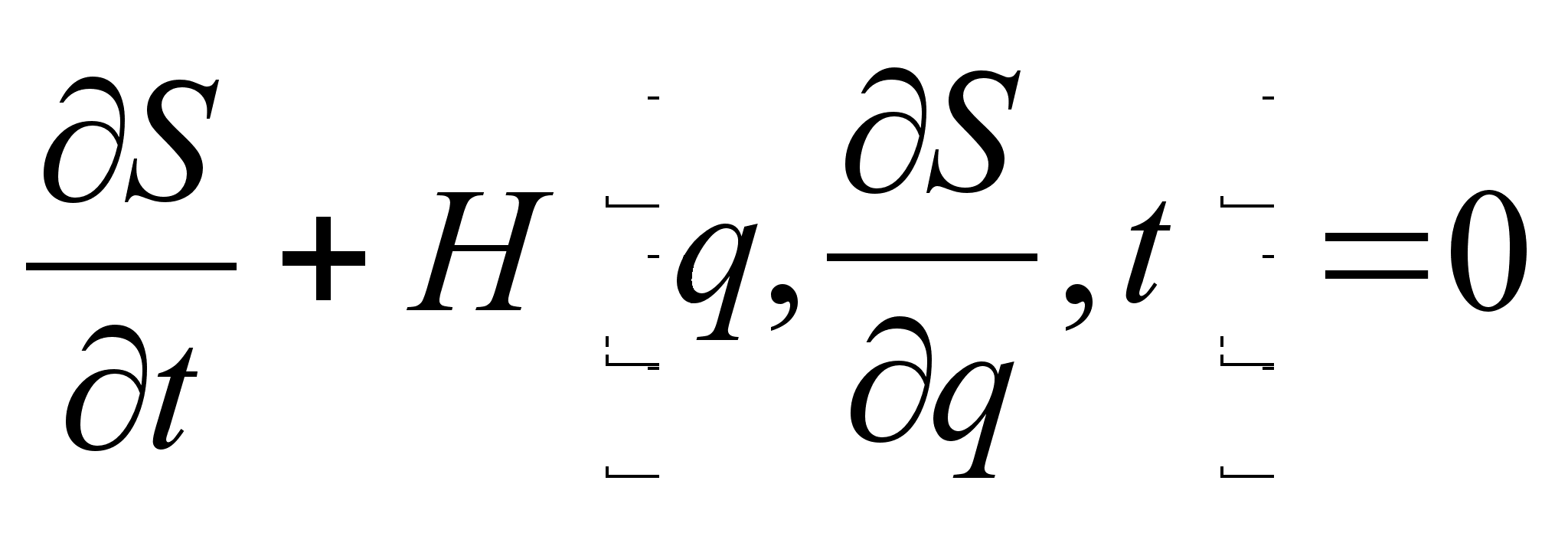
Здесь действие рассматривается как функция координат и времени: .

Путем интегрирования уравнения Гамильтона-Якоби , находят представление действия в виде полного интеграла, который является функцией s координат, времени, и s+1 постоянных (s – число степеней свободы). Поскольку действие входит в уравнение Гамильтона-Якоби только в виде производной, то одна из констант содержится в полном интеграле аддитивным образом, т.е. полный интеграл имеет вид:

Константа А не играет существенной роли, поскольку действие входит везде лишь в виде производной. А определяет, что, фактически, лишь s констант меняют действие существенным образом. Эти константы определяются начальными условиями на уравнения движения, которые для любого значения А будут иметь одинаковый вид, как и само уравнение Гамильтона-Якоби.

Для того чтобы выяснить связь между полным интегралом уравнения Г.-Я. и интересующими нас уравнениями движения, необходимо произвести каноническое преобразование, выбрав полный интеграл действия в качестве производящей функции.

Константы будут выступать в качестве новых импульсов. Тогда новые координаты

тоже будут константы, поскольку

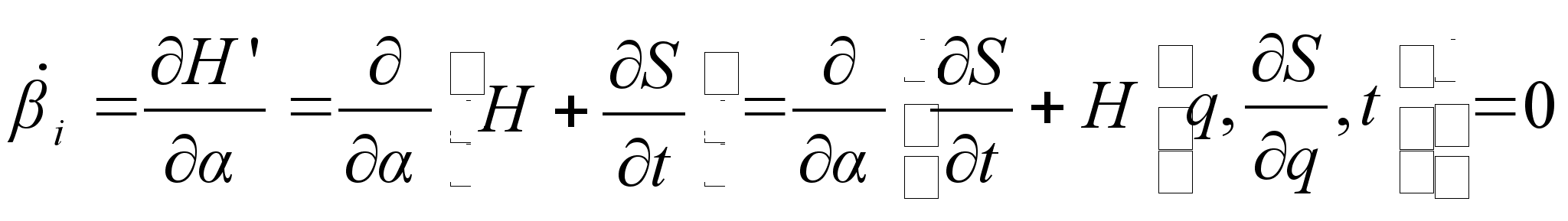
Выражая из уравнения координаты в виде функций от , мы и получим закон движения:

Решение задачи на нахождение зависимости существенно упрощается в случае разделения переменных. Такое возможно, когда какая-то координата может быть связана лишь с соответствующим ей импульсом и не связана ни с какими другими импульсами или координатами, входящими уравнение Г.-Я. В частности это условие выполняется для циклических переменных.

Итак, нахождение уравнений движения методом Гамильтона-Якоби сводится к следующему:

1. составить функцию Гамильтона;

2. записать уравнение Г.-Я., и определить какие переменные разделяются;

3. --> ЧИТАТЬ ПОЛНОСТЬЮ <--