Реферат: Теоретическая физика: механика
![]()
По определению обобщенных импульсов:
![]()
Откуда
![]()
Следовательно, по определению функция Рауса с учетом выражения :
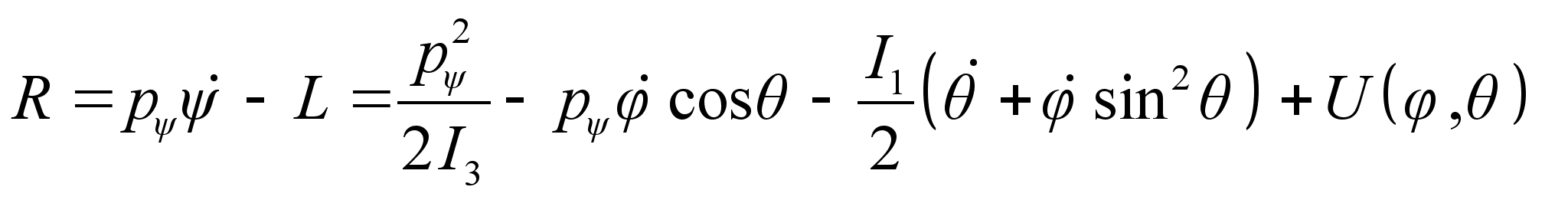
Домашнее задание:
Задача№1. Исходя из функции Гамильтона для гармонического осциллятора, получить закон движения гармонического осциллятора.
№49.7 []
№10.5 [] Найти уравнения движения частицы, функция Гамильтона которой: ![]() .
.
Указание: получить ![]() .
.
Литература:
-
Л.Д. Ландау, Е.М. Лифшиц «Механика, электродинамика», - М.: «Наука», 1969 г., - 272 с.
-
Л.Д. Ландау, Е.М. Лифшиц «Механика», - М.: «Наука», 1965 г., - 204 с.
-
И.И. Ольховский, Ю.Г. Павленко, Л.С. Кузьменков «Задачи по теоретической механике для физиков», - М.: 1977 г., - 389 с.
-
Г.Л. Коткин, В.Г. Сербо «Сборник задач по теоретической механике», - М.: «Наука», 1977 г., - 320 с.
-
И.В. Мещерский «Сборник задач по теоретической механике», - М.: «Наука», 1986 г., - 448 с.
-
Л.П. Гречко, В.И. Сугаков, О.Ф. Томасевич, А.М. Федоренко «Сборник задач по теоретической физике», - М.: «Высшая школа» 1984 г., - 319 с.
Студент-практикант: Филатов А.С.
| “Согласовано” | “Утверждено” |
|
Преподаватель Джежеря Ю.И. ___________ | Методист ____________________ |
План-конспект занятия
По теоретической физике
Студента V курса физико-математического факультета, гр. ОФ-61
Филатова Александра Сергеевича
Дата проведения занятия: 27.12.2000
Тема: «Функция Гамильтона-Якоби. Разделение переменных»
Цели: Закрепить умение использования метода Гамильтона-Якоби при решении задач с разделением переменных. Сформировать понимание сути и могущественности метода. Воспитывать трудолюбие, прилежность.
Тип занятия: практическое.
Ход занятия
Краткие теоретические сведения
При рассмотрении действия, как функции координат (и времени), следует выражение для импульса:
![]()