Реферат: Теоретическая физика: механика

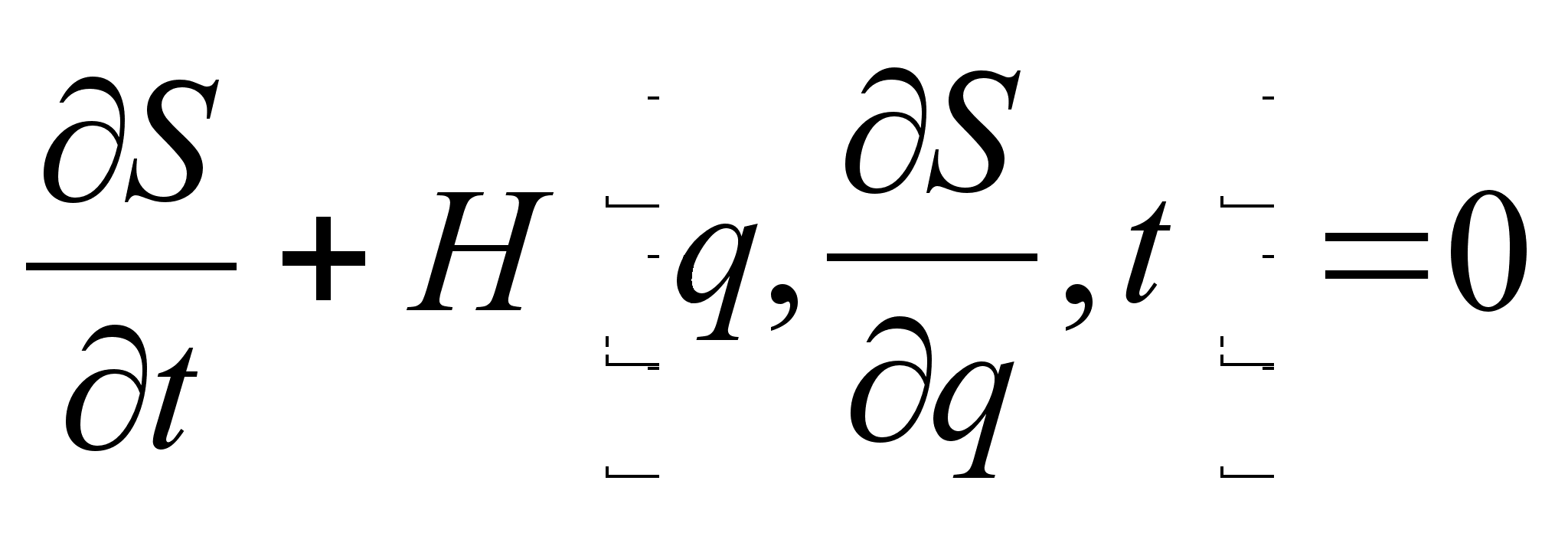
Здесь действие рассматривается как функция координат и времени: .

Путем интегрирования уравнения Гамильтона-Якоби , находят представление действия в виде полного интеграла, который является функцией s координат, времени, и s+1 постоянных (s – число степеней свободы). Поскольку действие входит в уравнение Гамильтона-Якоби только в виде производной, то одна из констант содержится в полном интеграле аддитивным образом, т.е. полный интеграл имеет вид:

Константа А не играет существенной роли, поскольку действие входит везде лишь в виде производной. А определяет, что, фактически, лишь s констант меняют действие существенным образом. Эти константы определяются начальными условиями на уравнения движения, которые для любого значения А будут иметь одинаковый вид, как и само уравнение Гамильтона-Якоби.

Для того чтобы выяснить связь между полным интегралом уравнения Г.-Я. и интересующими нас уравнениями движения, необходимо произвести каноническое преобразование, выбрав полный интеграл действия в качестве производящей функции.

Константы будут выступать в качестве новых импульсов. Тогда новые координаты

тоже будут константы, поскольку

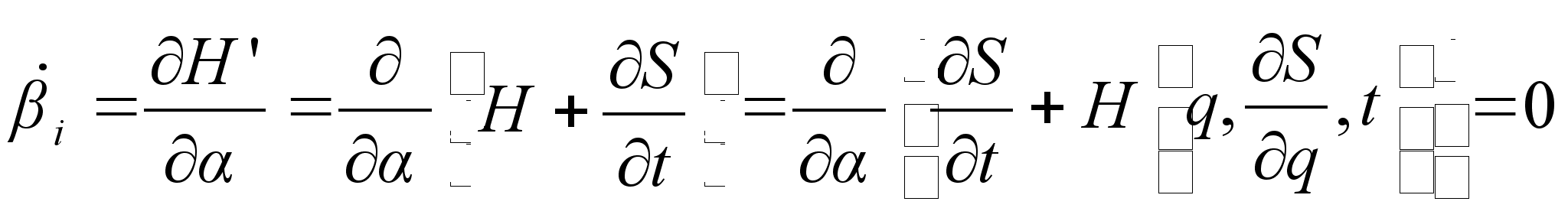
Выражая из уравнения координаты в виде функций от , мы и получим закон движения:

Решение задачи на нахождение зависимости существенно упрощается в случае разделения переменных. Такое возможно, когда какая-то координата может быть связана лишь с соответствующим ей импульсом и не связана ни с какими другими импульсами или координатами, входящими уравнение Г.-Я. В частности это условие выполняется для циклических переменных.

Итак, нахождение уравнений движения методом Гамильтона-Якоби сводится к следующему:

1. составить функцию Гамильтона;

2. записать уравнение Г.-Я., и определить какие переменные разделяются;

3. Путем интегрирования уравнения Г.-Я. получить вид полного интеграла ;

4. Составить систему s уравнений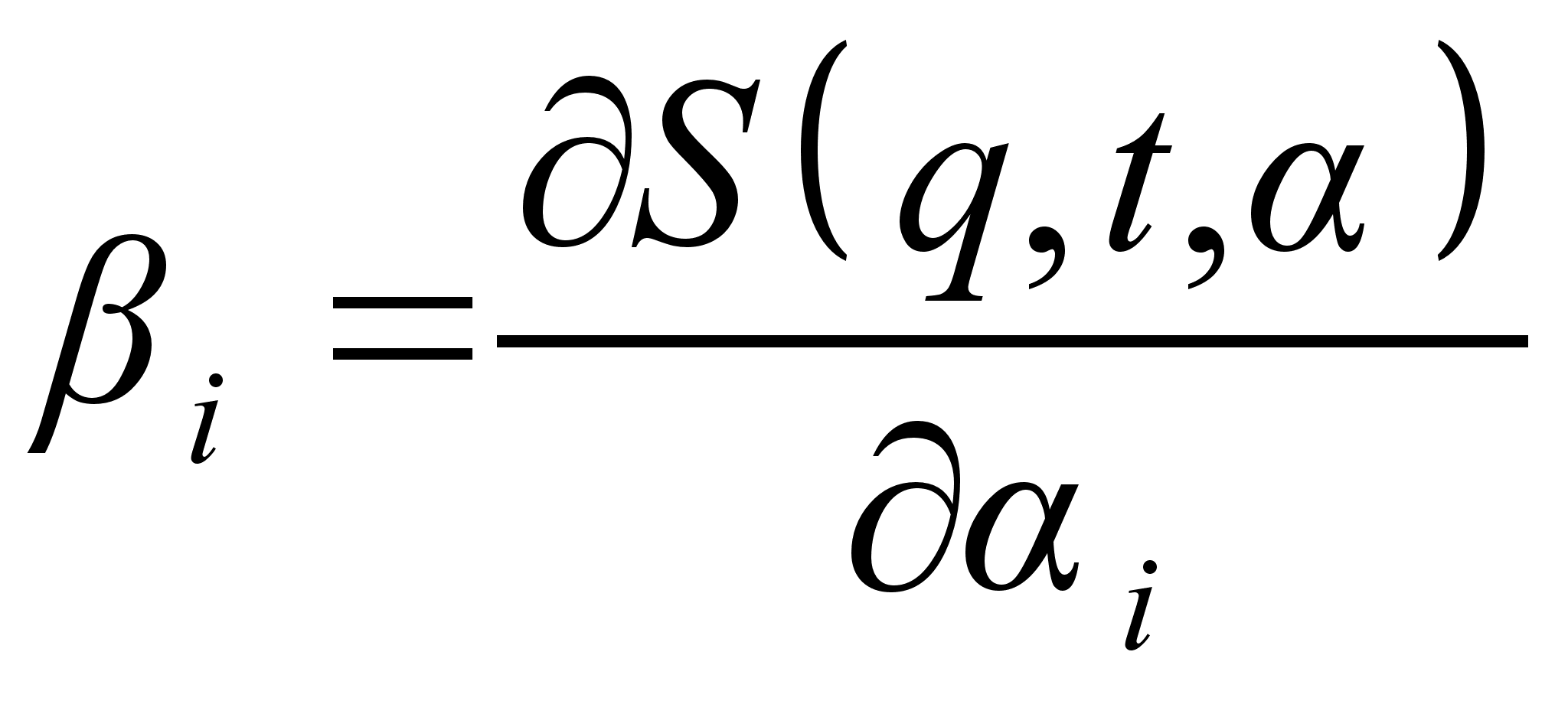, и получить закон движения ;

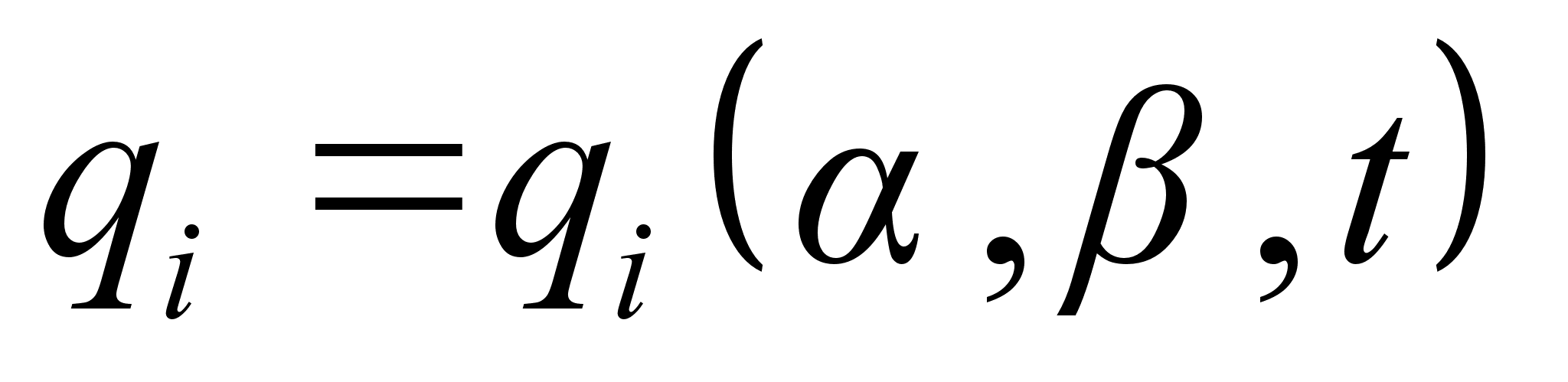5. По необходимости найти закон изменения импульсов: 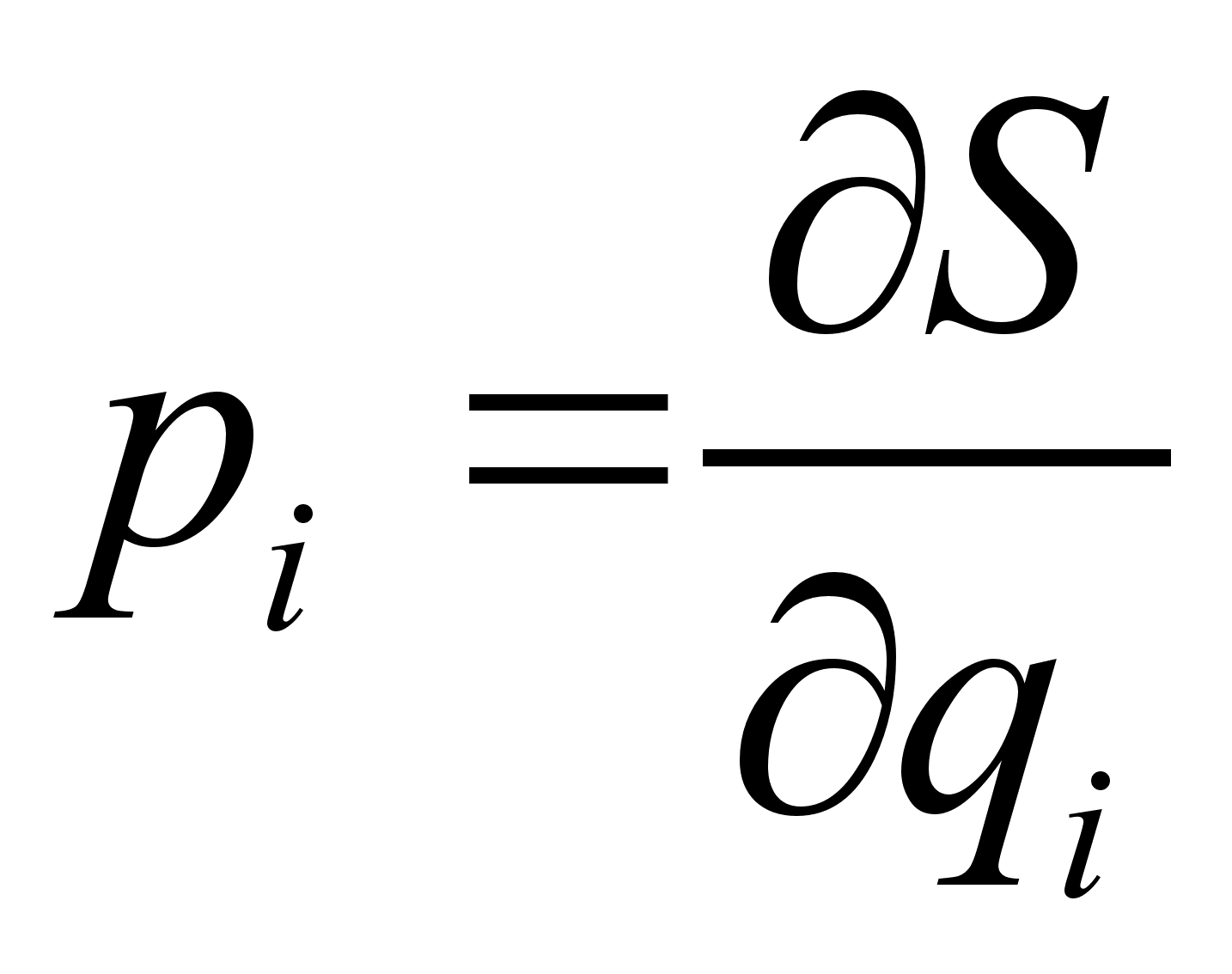. Для чего продифференцировать полный интеграл по координатам 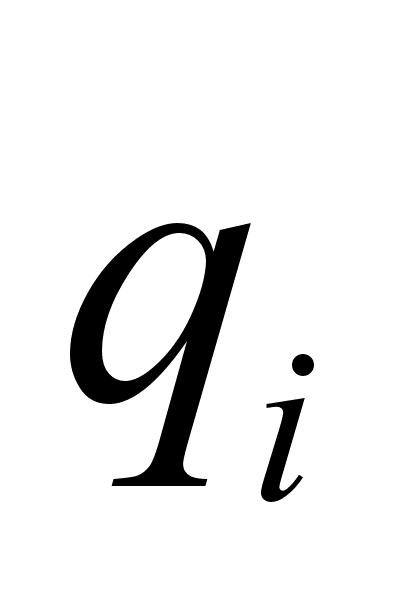, а потом подставить их явный вид, полученный в пункте 4.

Примеры решения задач

На прошлом занятии был продемонстрирован пример нахождения закона движения для свободной точки. Что же будет происходить при помещении точки в поле?

№9.22 [] Составить уравнения Г.-Я. для точки, движущейся в однородном гравитационном поле. Найти полный интеграл этого уравнения, а также траекторию и закон движения точки.

Решение:

1. Направим ось Oz вверх по вертикали. Тогда функция Гамильтона точки в декартовых координатах примет вид:

2. Соответственно уравнение Г.-Я.:

3. Все переменные в этом уравнении разделяются. Здесь . Разделение переменных позволяет нам представить действие в виде суммы:

Тогда, к примеру, изменение х, повлечет за собой изменение лишь первого слагаемого в квадратных скобках уравнения . Слагаемое может меняться, а все выражение все равно тождественный ноль. Следовательно, это слагаемое есть константа.