Реферат: Теоретическая физика: механика

Примеры решения задач

№10.3 [] Определить функцию Гамильтона ангармонического осциллятора, функция Лагранжа которого:

Решение:

Откуда

Подставляя полученное выражение в , имеем:

№49.8 [] Материальная точка массы т подвешена с помощью стержня длины к плоскому шарниру, горизонтальная ось которого вращается вокруг вертикали с постоянной угловой скоростью . Составить а) функцию Гамильтона и б) канонические уравнения движения. Массу стержня не учитывать.

Решение:

а) 1. Действуя согласно предлагаемой схеме составления функции Гамильтона, определим функцию Лагранжа системы:

Где . Поскольку функция Лагранжа определена с точностью до аддитивной константы, либо постоянного множителя, перепишем в виде:

Согласно выбранной системе координат:

Учитывая, что – по условию, получим выражение для функции Лагранжа с новой обобщенной координатой :

Или

2. Найдем зависимость обобщенной скорости от обобщенного импульса системы. По определению обобщенных импульсов:

3. Следовательно, функция Гамильтона:

б) Используя формулы , найдем уравнения движения системы:

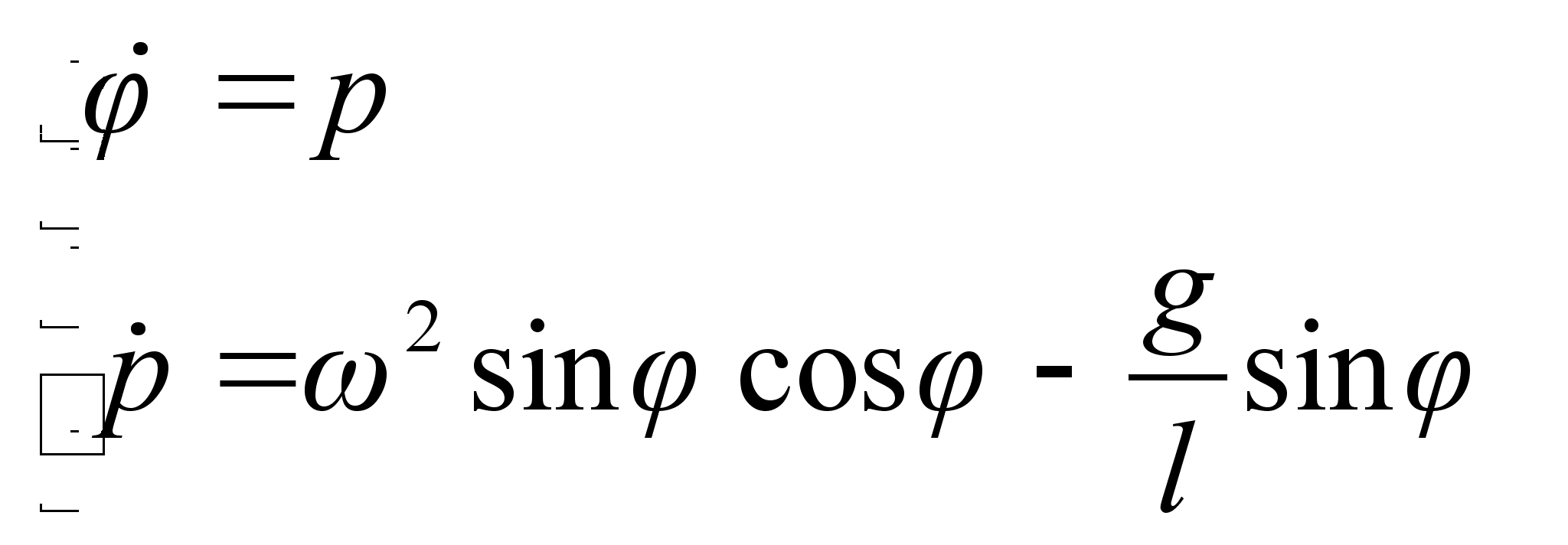
В частности, представляет интерес случай, когда , т.е. шарик движется в горизонтальной плоскости, описывая окружность. Логично предположить, что такое движение будет выполняться лишь при некотором фиксированном угле , значение которого как-то зависит от параметров системы. Найдем эту зависимость. Для этого заметим, что во втором уравнении системы левая часть будет равна нулю: