Реферат: Теоретическая физика: механика

Откуда:

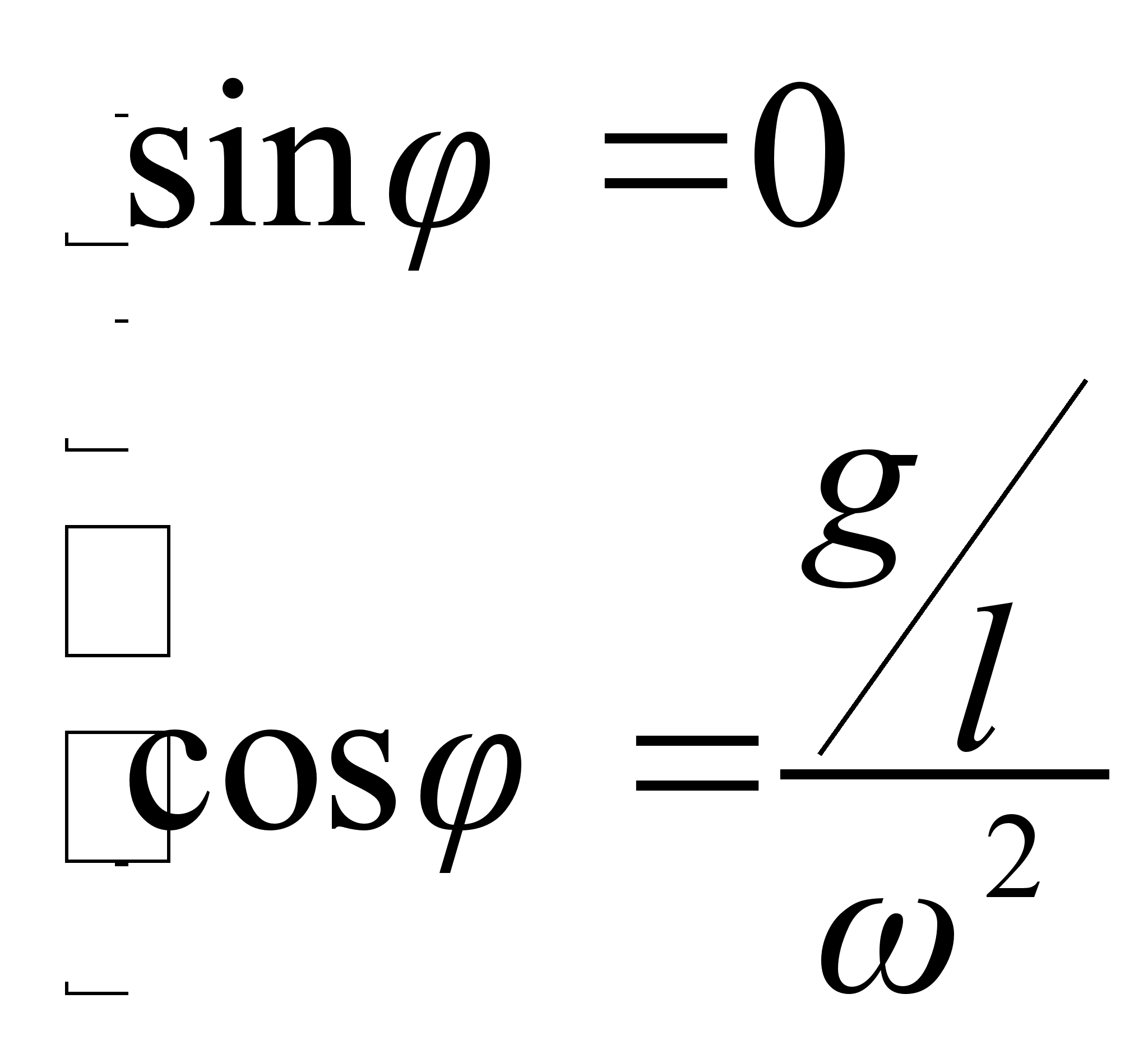
Первое уравнение дает тривиальное решение , что соответствует просто провисанию шарика - материальной точки. Т.о. условие движения маятника в плоскости есть:

Где – собственная частота колебаний маятника. Более того, выражение дает зависимость угла отклонения, обуславливающего движение в плоскости, от частоты вращения вертикальной оси, и собственной частоты маятника. Т.о., чтобы добиться устойчивого вращения в плоскости при желаемом угле отклонения, необходимо подбирать отношение между собственной частотой (которая определяется длинной стержня) и частотой вращения оси. Заметим также, что значение угла в этом случае не зависит от массы маятника. При значении частоты вращения вертикальной оси, превышающим значение собственной частоты маятника, второе уравнение системы решений не имеет. Но работает первое уравнение, из которого . Т.е. маятник будет провисать.

№9.5 [] Найти траекторию одномерного гармонического осциллятора в фазовом пространстве.

Решение:

Фазовым пространством называется такое 2s-мерное пространство, по осям которого откладываются s импульсов и s координат. (s – число степеней свободы). Изменение состояния системы соответствует непрерывной линии – траектории движения системы в фазовом пространстве.

Функция Гамильтона гармонического осциллятора имеет вид:

Из закона сохранения энергии получим уравнение фазовой траектории гармонического осциллятора:

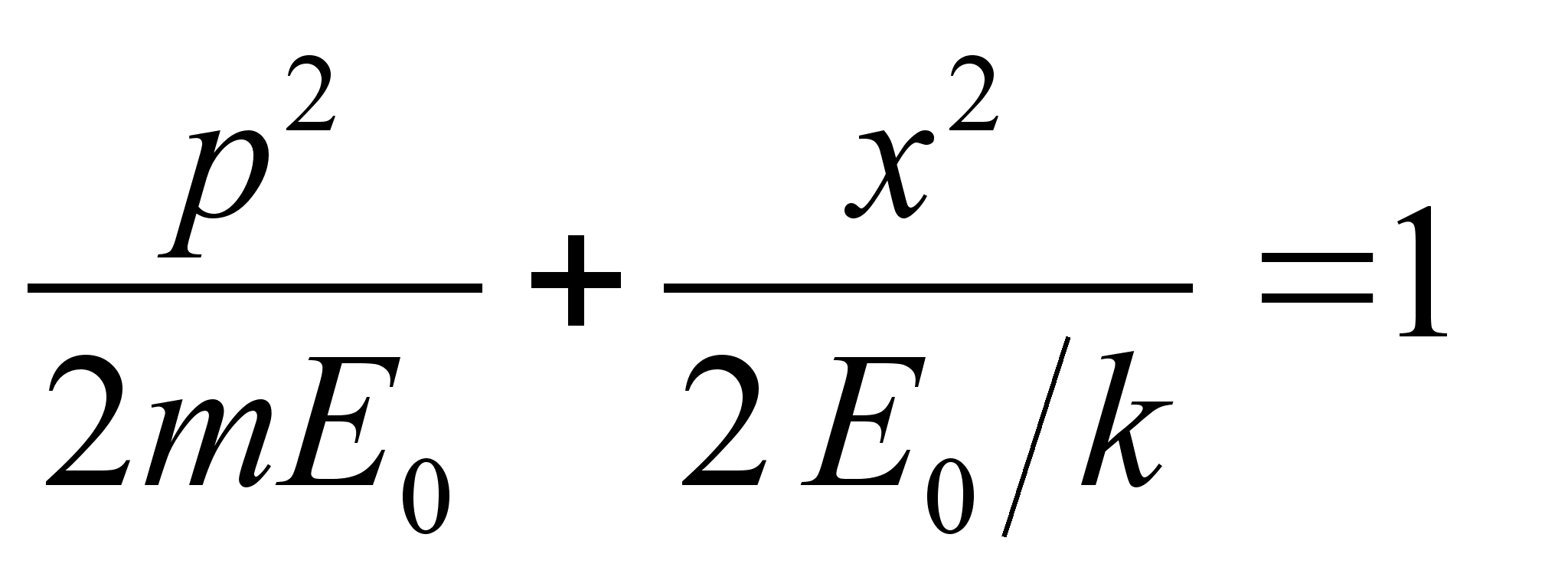
Т.е. траекторией является эллипс.

№10.4 [] Найти закон движения частицы, функция Гамильтона которой:

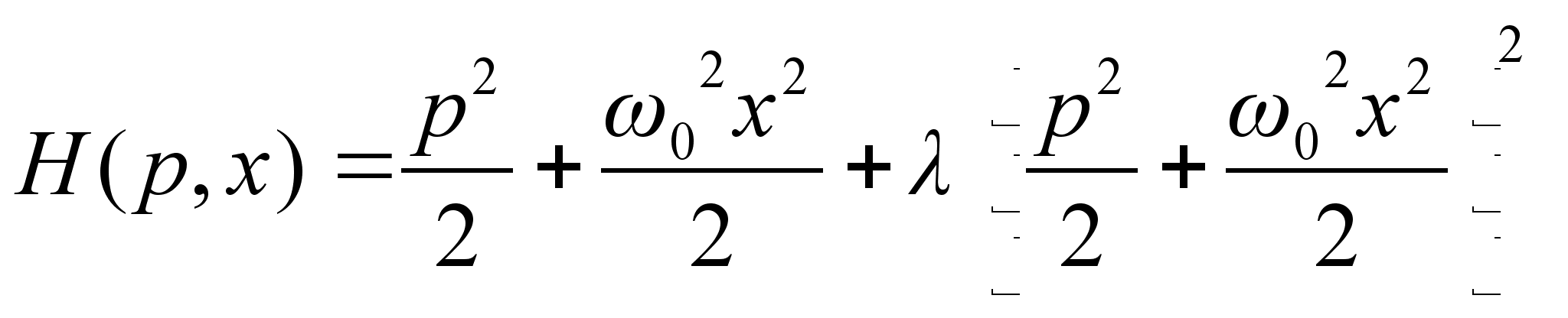
Решение:

Закон движения частицы дают функции:

,

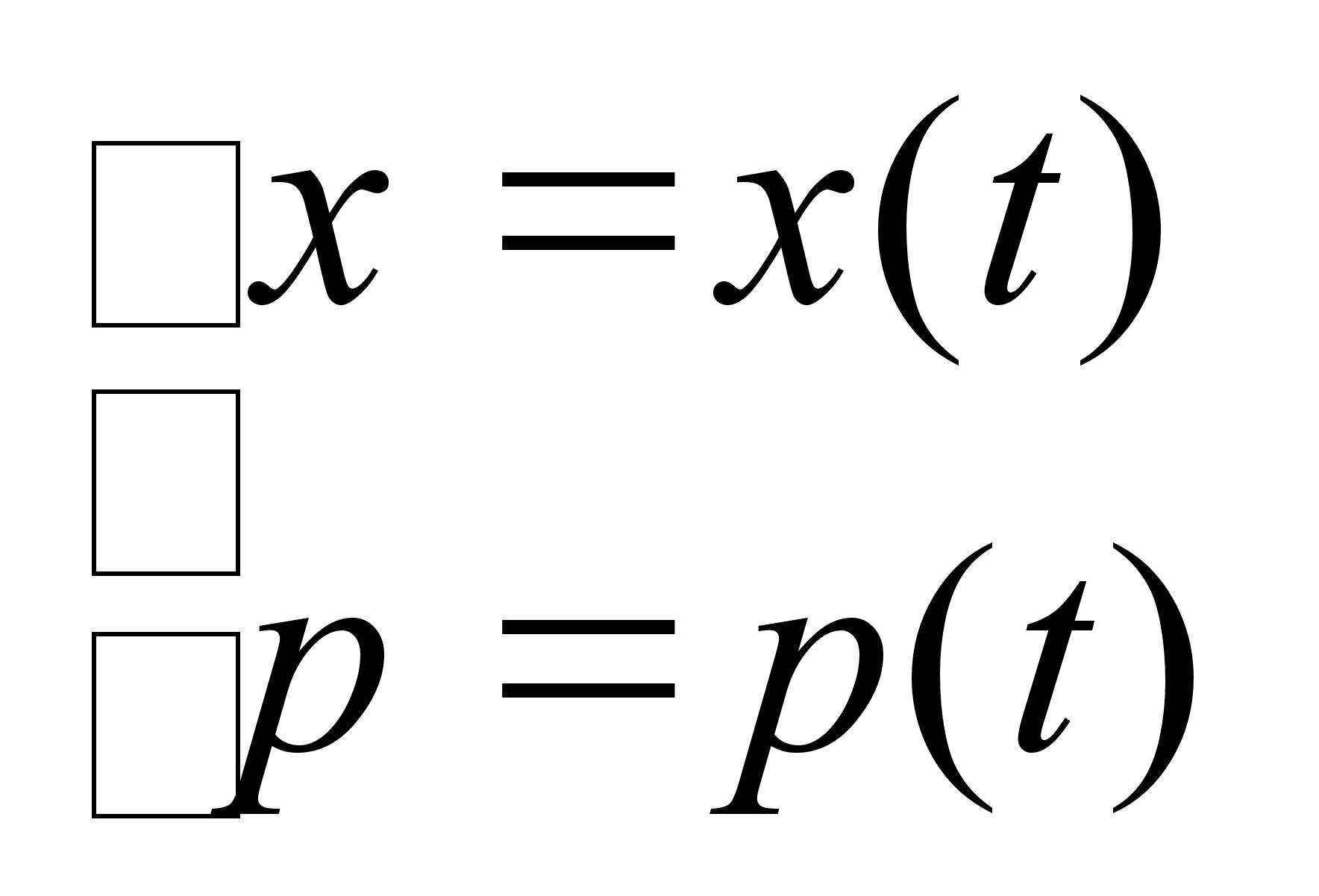вид которых можно получить исходя из уравнений Гамильтона . Поделив 1-ое уравнение на 2-ое получим:

,

откуда

Интегрируя, получим:

Выражая отсюда и приравнивая его к значению из уравнения Гамильтона, получим:

,

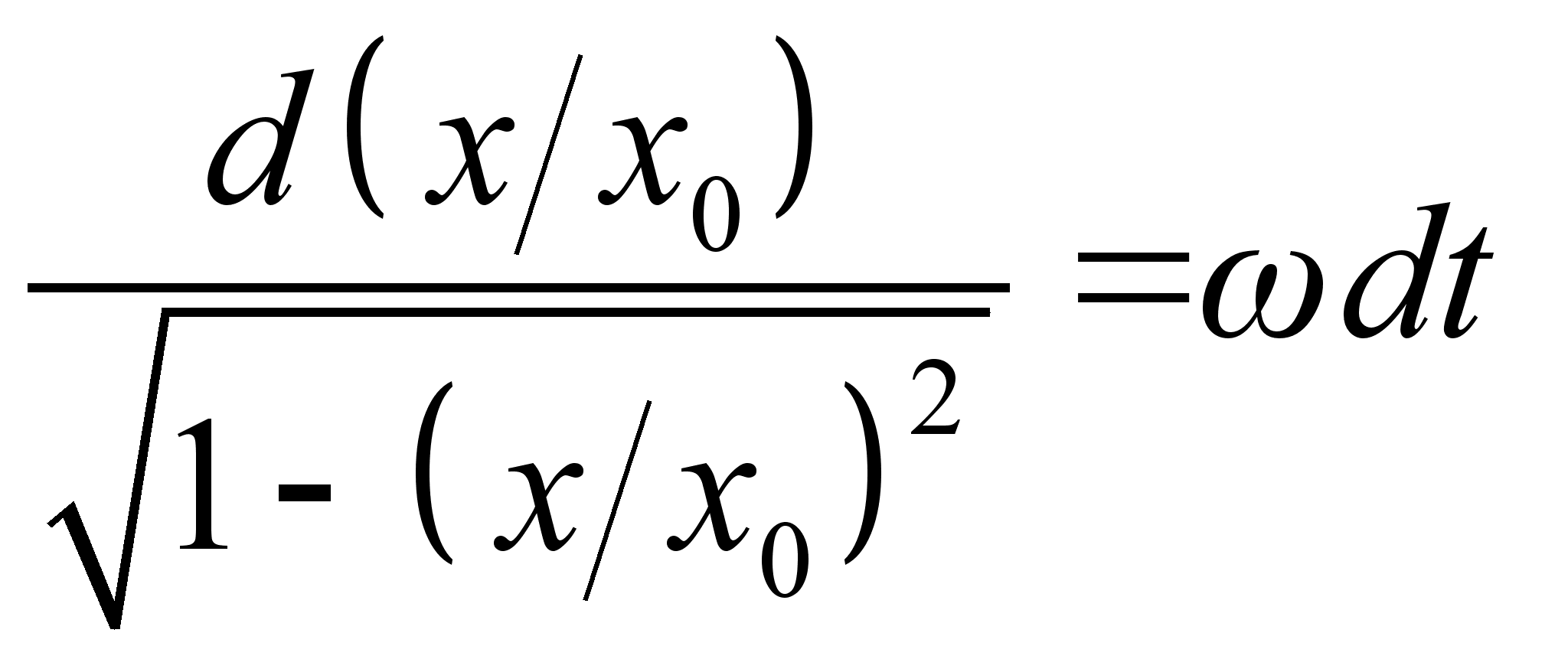где

Или после интегрирования: