Реферат: Теория автоматического управления 2

Вычисляем квадратичную интегральную оценку:

Задаваясь численными значениями kрк , составляем таблицу зависимости квадратичной интегральной оценки от коэффициента kрк , которая приведена ниже.
Таблица 5. – Расчетные данные для построения кривой зависимости интегральной оценки от передаточного коэффициента разомкнутого контура
| крк | Qкв |
| 1 | 1.074 |
| 2 | 0.629 |
| 3 | 0.483 |
| 4 | 0.414 |
| 5 | 0.374 |
| 6 | 0.349 |
| 7 | 0.335 |
| 8 | 0.325 |
| 9 | 0.319 |
| 10 | 0.317 |
| 11 | 0.317 |
| 12 | 0.319 |
| 13 | 0.322 |
| 14 | 0.327 |
| 15 | 0.333 |
| 20 | 0.389 |
| 25 | 0.498 |
| 30 | 0.736 |
| 35 | 1.521 |

Рис. 9 - Кривая зависимости интегральной оценки от передаточного коэффициента разомкнутого контура
При помощи программы Matlab вычислим минимум функции Qкв на интервале [1;35], он равен 10,56. Следовательно, оптимальным значением kрк является kрк =10,56. При данном значении коэффициента разомкнутого контура система будет работать в оптимальном режиме, обеспечивая минимальную площадь под графиком переходного процесса.
Теперь перейдем от коэффициента kрк к передаточному коэффициенту kу . Для этого воспользуемся следующей формулой:
![]()
При коэффициенте kрк =10,56 и квадратичной интегральной оценке равной Q=0.3166 передаточный коэффициент управляющего устройства kу .= 45,8.
Вывод: В этом разделе с помощью квадратичной интегральной оценки получили оптимальное значение передаточного коэффициента управляющего устройства (kу =45,8). Этот коэффициент получился меньше, чем тот, что был выбран в разделе 2 (kу =56,3). Следовательно, при выборе этого коэффициента точность системы в установившемся режиме увеличится, но могут получиться более колебательные переходные процессы.
7. Вычисление и минимизация дисперсии сигнала ошибки при случайных воздействиях
Дисперсия сигнала ошибки De при действии на систему внешних некоррелированных воздействий хз и g может быть представлена суммой:
![]()
где Deз – дисперсия, обусловленная неточным воспроизведением задающего воздействия;
Deg – дисперсия, обусловленная неполным подавлением помех.
Вычислим дисперсию, обусловленную неточным воспроизведением задающего воздействия:

где Sхз (ω) – спектральная плотность полезного сигнала
![]()
Запишем передаточную функцию замкнутого контура по каналу ошибки хз -ε.
![]()
![]()
Заменяем р на jω:
![]()
Подставим это выражение в формулу дисперсии, обусловленной неточным воспроизведением задающего воздействия:

 =
=
=![]()
 =
=

где
![]()
![]()
![]()
Подставим это выражение в формулу дисперсии, обусловленной неточным воспроизведением задающего воздействия:
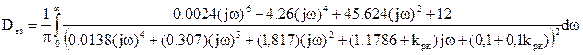
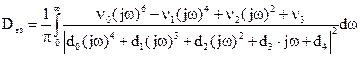
Вычисление дисперсии неточного задающего воспроизведения вычислим по формуле:
![]()
Запишем коэффициенты vi и di для составления определителей Δ и Δv :
v0 =0.0024 d0 =0.0138