Реферат: Використання комп’ютерів у фізиці

Ілюструємо класичні методи і метод Монте-Карло для оцінки чисельних інтегралів.

10.1. Прості одномірні методи чисельного інтегрування.

Ці методи (класичні) мають перевагу для малих розмірностей.

Геометрична інтерпретація інтегралу - площа під графіком у межах x = a до x = b, відрізок ділимо на n відрізків довжиною :

де , і ,

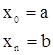
Оцінка площі - сума площ прямокутників. Значення обчислюється у початку відрізків і оцінка інтегралу дається формулою:

.

10.2. Інший метод трапеції із сторонами у початку і кінці відрізка.

Тобто, f(x) замінюємо прямою, що сполучає значення f(x) в кінцях відрізка. Площа

.

Повна площа

.

Більшу точність дає квадратична, або параболічна інтерполяція за трьома точками

Площа під параболою між точками виражається формулою:

Повна площа всіх параболічних сегментів:

,

де n – має бути парним.

.

Точність методу прямокутників зростає, як = , трапецій – n^-2 , парабол – n^-4 .

10.3.Чисельне інтегрування багатовимірних інтегралів.

Багато фізичних задач містять усереднення по багатьом змінним. Наприклад, середнє значення енергії системи частинок E(r_i ,p_i ), i =1, ..., n. Якщо розмірність простору N = 6n, а число точок на відрізку одного виміру p, то потрібно обчислити за p^N точками суму.

Ще дуже складно визначати N-1 - межу інтегрування. Стандартні методи використовуються для N = 2 - 5.

Найпростіший метод оцінки багатовимірних інтегралів зводиться до послідовного взяття одновимірних інтегралів:

,

і .

10.4. Обчислення інтегралів найпростішим методом Монте-Карло.