Реферат: Використання комп’ютерів у фізиці

легко показати що

Хвильове рівняння має величезну кількість розв’язків наприклад

Оскільки хвильове рівняння лінійне, то розв’язок можна представити у вигляді ряду Фур’є.

Якщо хвиля при русі зберігає свою форму то кажуть, що вона не диспергує, це зумовлено лінійністю зв’язку i k, інакше кожна гармоніка хвилі рухається з тією ж швидкістю. Якщо ж швидкість хвилі залежить від довжини хвилі (або хвильового числа), то кажуть, що диспергує, і цьому випадку форма хвилі змінюється з часом.

8.5. Інтерференція і дифракція.

Про інтерференцію говорять, коли змішуються хвилі від невеликого числа джерел, а про дифракцію коли від великого.

Дослід Юнга.

Дві щілини, монохроматичне світло. Щілини як точкові джерела

.

Електричне поле буде рівне сумі

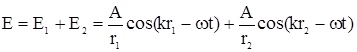
Інтенсивність дорівнює .

8.6. Поляризація.

Розглянемо явище, коли цікавить напрямок коливань. Для поперечної електромагнітної хвилі. Напруженість двовимірна векторна функція вздовж z-розповсюджується хвиля.

E_x (z,t) і E_y (z,t) Для монохроматичної хвилі =const, але компоненти коливаються незалежно.

Щоб сумарне поле знайти треба векторно скласти компоненти.

8.7. Геометрична оптика і принцип найменшого часу.

Геометричною оптикою можна користуватись, коли <<l, l – розмір перепон чи детекторів.

Для променів, що розповсюджуються, виконується принцип Ферма: промінь світла йде по шляху між двома точками, який вимагає найменшого часу.

Аналогічний принцип найменшої дії використовується замість законів Ньютона у якості фундамента всієї класичної механіки. В однорідному середовищі світло поширюється прямолінійно.

Розглянемо дзеркало:

a + b = d

Цікавим є застосування принципа Ферма для задач заломлення, коли світло падає на поверхню розділу двох речовин, у яких швидкість світла різна: