Реферат: Використання комп’ютерів у фізиці

можемо генерувати розподілами за експоненційним законом, а рівномірно в межах [0,2] то змінні будуть розподілені за нормальним законом з нульовим середнім і дисперсією .

10.8. Вибірка за значимістю (суттєва вибірка).

Похибка методу Монте-Карло пропорційна , познайомимось з методом зменшення . Введемо додатню Р(х) таку, що 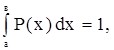тоді

можна переписати у такому виді

.

Обчислимо інтеграл 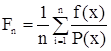, виконуючи вибірку у відповідності до розподілу Р(х), при рівномірному Р(х)=1/(в-а).

Вибираємо Р(х), що веде себе подібно до f(x) там де f(x) велика, тому підінтегральний вигляд буде функцією, що слабо змінюється і дисперсія буде малою.

10.9 Метод випадкового блукання (метод Метрополіса)

Метод одержання не рівномірного розподілу полягає у тому , що деякі вибірки відкладаються.

Нехай хочемо генерувати змінні з розподілом Р(х).

Випадкове блукання задається імовірністю переходу w(x_i x_j ) від одного x_i до іншого x_j для того, щоб розподіл точок x₀ , x₁ , x₂ ,… сходився до Р(х).

Можна показати, що достатньо задовольняти умові детального балансу

Р(х_і ) w(x_i x_j )=P(х_j ) w(x_j x_i ),

де співвідношення не задає однозначного w(x_j x_i ).

Розглянемо найпростіший варіант

w(x_j x_i ) = min.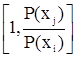

Перехід можна описати наступними кроками, нехай пішохід знаходиться в точці з координатою х_n .

Для отримання х_n+1 :

Вибираємо пробну координату x_t = х_{n +} _n .

Обчислюємо w =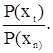

Якщо w1, приймаємо цей перехід і кладемо х_n+1 =x_t .

Якщо w<1, генеруємо випадкове r.

Якщо rw, приймаємо цей перехід і кладемо х_n+1 =x_t .

Якщо r>w, не приймаємо і х_n+1 =x_n .

беруть таким, щоб приймалось від 1/3 до 1/2 кроків. Починають блукання з х для якого Р(х) максимальне.