Реферат: Використання комп’ютерів у фізиці

Нехай r – випадкове число, рівномірно розподілене на одиничному інтервалі [0,1] з густиною ймовірності:

.

Наше завдання знайти зв’язок між x i r_, такий, що якщо r рівномірно розподілено, то х за законом p(x). Зв’язок встановлюють через інтегральну функцію розподілу:

,

де Р(x) – інтегральна функція розподілу, яка рівна ймовірності одержання випадкового числа меншого за х.

Зв’язок має вигляд:

.

Випадкова величина P(x) розподілена рівномовірно.

.

Ймовірність знайти x в інтервалі , рівна dP(x).

Співвідношення між dP(x) і dx можна знайти

отже в межах 0r1 маємо dP(x)=P(x) dx=P_u (r) dr

Бачимо, що х розподілено з бажаною густиною імовірності.

Приклади:

Згенеруємо рівномірно розподілені на [a, b] числа. Шукана густина

P(x) = r

x = P^-1 (r), , x= a + (в-a) r.

Змінна розподілена за законом (1), коли r—рівномовірне.

Інший випадок

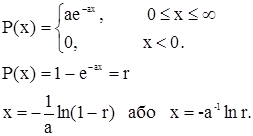
Однак метод оберненого перетворення може бути не найефективнішим. Для використання методу має виконуватись два співвідношення, має братись інтеграл Р(х) і розв’язуватись співвідношення Р(х)=r відносно х.

Для цього зробити не можна.

Однак можна згенерувати двовимірний гаусів розподіл

перейдемо до полярних координат.

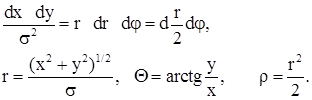
знайдемо імовірність у вигляді: