Реферат: Випадкові події

Якщо , то розглядається ймовірність попадання точки в точку на відрізку . Як слідує з (1), така ймовірність дорівнює нулю:

.

Отже, якщо ймовірність події дорівнює нулю, то необов’язково, що ця подія неможлива.

Нехай g – плоска фігура, яка цілком знаходиться всередині іншої плоскої фігури G. На фігуру G навмання кидається точка. Це означає виконання таких допущень:

– кинута точка може опинитись у будь-якій точці фігури G;

– ймовірність попадання точки на фігуру g пропорційна площі цієї фігури і не залежить ні від її розташування відносно фігури G, ні від її форми.

За таких умов ймовірність попадання точки у фігуру g дорівнює відношенню площ фігур:

,(2)

– площа фігури g, – площа фігури G.

Означення (1) та (2) є частковими випадками загального означення геометричних ймовірностей:

,(3)

де mes позначає міру (площу, об’єм, довжину) області, – вектор, який визначає точку у n-вимірному евклідовому просторі.

Приклад 1. У сигналізатор поступають сигнали з двох пристроїв. Надходження сигналів від пристроїв рівноможливе у будь-який момент часу на проміжку від 0 до Т. Моменти надходження сигналів незалежні один від одного. Сигналізатор спрацьовує, якщо різниця між моментами надходження сигналів менша ніж t . Знайти ймовірність того, що сигналізатор подасть сигнал за час Т (подія A), якщо кожен із пристроїв надішле по одному сигналу.

Розв’язування. Нехай моменти надходження сигналів від першого й другого пристроїв відповідно x та y. За умовою задачі

(*)

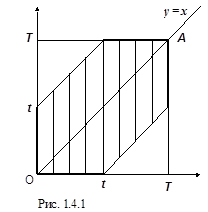
Нерівностям (*) задовільняють координати будь-якої точки квадрату ОТАТ (рис. 1). Отже, цей квадрат можна розглядати як фігуру G. Його площа . Сигналізатор подає сигнал, якщо різниця між моментами надходження сигналів менша за t;

, якщо ,(**)

, якщо .(***)

Нерівність (**) виконується для точок фігури G, які знаходяться вище прямої і нижче прямої ; нерівність (***) має місце для точок, які знаходяться нижче прямої і вище прямої . Як видно з рис.1 нерівностям (**) та (***) одночасно задовільнять точки заштрихованого шестикутника, який можна прийняти в якості фігури g. Його площа . За формулою (2)

5 . Статистичне означення ймовірностей

Статистичне означення ймовірності базується на спостереженнях за випадковою подією при послідовності експериментів.

Нехай експеримент S повторено n разів і подія A у цьому конкретному експерименті настала m разів. Відношення

(1)

називається відносною частотою випадкової події.

Відносна частота змінюється від серії до серії з n експериментів, але має властивість стійкості. Це означає, що у різних серіях із достатньої великої кількості експериментів, відносна частота змінюється мало (тим менше, чим більше виконано експериментів у серії), коливаючись біля деякого постійного числа, близьким до ймовірності події А.

Тому відносну частоту можна прийняти за наближене значення ймовірності:

.(2)

Наближена рівність (2) є тим точніша, чим більше n.