Реферат: Вычислительные методы алгебры (лекции)

.

Функция непрерывная в окрестности корня уравнения (1). Следовательно, уравнение (1) и уравнение (2) будут иметь один и тот же корень .

В качестве выберем , тогда (3)

Выберем начальное приближение достаточно близкое к . Остальные приближения получаются по формуле:

(4)

Метод, определенный (4), называется методом Ньютона.

Докажем, что метод Ньютона сходится и получим его оценку погрешности.

Если дано, что , где – символ Ландау:

если k=1, то скорость сходимости линейная;

если k=2, то скорость – квадратичная;

если k=3, то скорость – кубическая;

если k>1, то сходимость метода сверхлинейная.

Докажем, что (4) сходится.

Для этого покажем, что отображение – сжатие, где .

.

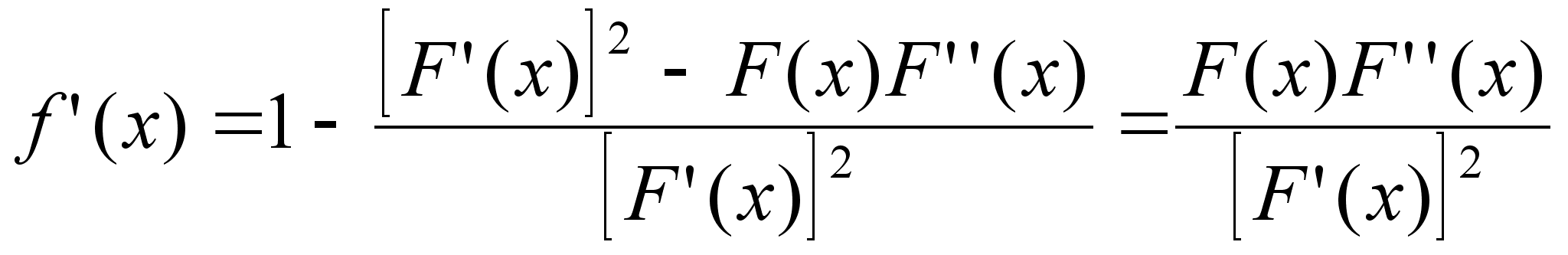При получим

.

По непрерывности функции на существует такая окрестность точки , что для , , а этом сжатие.

Поэтому к отображению можно применить принцип сжатыхотображений.

Если выбрать , то будет сходиться к точному решению уравнения (1)., т.е. .

Заметим, что метод (4) будет сходиться, если начальное приближение будем выбирать из окрестности

, .

Докажем, что метод Ньютона сходится.

Определим скорость сходимости метода Ньютона. Для этого разложим в ряд Тейлора в точке .

.

При имеем . Поэтому

Выразим (5)

Обозначим через ,