Шпаргалка: Действительные числа Иррациональные и тригонометрический уравнения
Сравнение a + bi = c + di означает, что a = c и b = d (два комплексных числа равны между собой тогда и только тогда, когда равны их действительные и мнимые части).
Сложение (a + bi ) + (c + di ) = (a + c ) + (b + d ) i .
Вычитание (a + bi ) − (c + di ) = (a − c ) + (b − d ) i .
Умножение
![]()
Деление 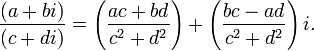
Числовая функция. Способы задания функции
В математике числовая функция - это функция, области определения и значений которой являются подмножествами числовых множеств - как правило, множества действительных чисел ![]() или множества комплексных чисел
или множества комплексных чисел ![]() .
.
Словесный: С помощью естественного языка Игрек равно целая часть от икс. Аналитический: С помощью аналитической формулы f (x ) = x !
Графический С помощью графика ![]() Фрагмент графика функции
Фрагмент графика функции ![]() .
.
Табличный: С помощью таблицы значений
|
x |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
y |
1 |
1 |
2 |
3 |
5 |
8 |
13 |
К-во Просмотров: 888
Бесплатно скачать Шпаргалка: Действительные числа Иррациональные и тригонометрический уравнения
|