Шпаргалка: Действительные числа Иррациональные и тригонометрический уравнения

4. Т = 2л - наименьший положительный период. Действительно,

sin (x+p) = sinx.

5. Точки пересечения с осями координат:

с осью Ох: sinx = 0; х = pn, nÎZ;

с осью Oy: если х = 0, то у = 0,6. Промежутки знакопостоянства:

sinx > 0 , если xÎ (2pn; p + 2pn), nÎZ;

sinx < 0 , если хÎ (p + 2pn; 2p+pn), nÎZ.

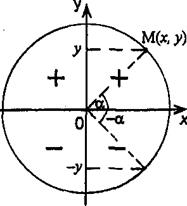
Знаки синуса в четвертях

у > 0 для углов а первой и второй четвертей.

у < 0 для углов ее третьей и четвертой четвертей.

7. Промежутки монотонноти:

y = sinx возрастает на каждом из промежутков [-p/2 + 2pn; p/2 + 2pn],

nÎz и убывает на каждом из промежутков [p/2 + 2pn; 3p/2 + 2pn], nÎz.

8. Точки экстремума и экстремумы функции:

x_max = p/2 + 2pn, nÎz; y _max = 1;

y_max = - p/2 + 2pn, nÎz; y_min = - 1.

Свойства функции у = cosx и ее график:

Свойства:

1. D (y) = R.

2. Е (у) = [-1; 1].

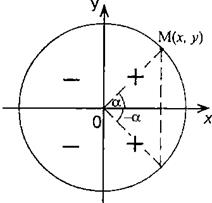
3. Функция у = cosx - четная, так как по определению косинуса тригонометрического угла cos (-a) = x/R = cosa на тригонометрическом круге (рис)

4. Т = 2p - наименьший положительный период. Действительно,

cos (x+2pn) = cosx.

5. Точки пересечения с осями координат:

с осью Ох: cosx = 0;

х = p/2 + pn, nÎZ;