Шпаргалка: Действительные числа Иррациональные и тригонометрический уравнения

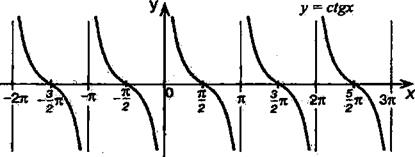
1. D (y) = (xÎR, x ¹ pn, nÎZ). 2. E (y) =R.

3. Функция y = ctgx - нечетная.

4. Т = p - наименьший положительный период.

5. Промежутки знакопостоянства:

ctgx > 0 при хÎ (pn; p/2 + pn;), nÎZ;

ctgx < 0 при хÎ (-p/2 + pn; pn), nÎZ.

Знаки котангенса по четвертям смотри на рисунке.

6. Функция у = ctgx возрастает на каждом из промежутков (pn; p + pn), nÎZ.

7. Точек экстремума и экстремумов у функции у = ctgx нет.

8. Графиком функции у = ctgx является тангенсоида , полученная сдвигом графика y= tgx вдоль оси Ох влево на p/2 и умножением на (-1) (рис)

Обратные тригонометрические функции, их свойства и графики

Обра́тные тригонометри́ческие фу́нкции (круговые функции , аркфункции ) - математические функции, являющиеся обратными к тригонометрическим функциям. К обратным тригонометрическим функциям обычно относят шесть функций: аркси́нус , аркко́синус , аркта́нгенс , арккотангес. Название обратной тригонометрической функции образуется от названия соответствующей ей тригонометрической функции добавлением приставки "арк-" (от лат. arc - дуга). Это связано с тем, что геометрически значение обратной тригонометрической функции можно связать с длиной дуги единичной окружности (или углом, стягивающим эту дугу), соответствующей тому или иному отрезку. Изредка в иностранной литературе пользуются обозначениями типа sin⁻¹ для арксинуса и т.п.; это считается не совсем корректным, так как возможна путаница с возведением функции в степень −1. Основное соотношение

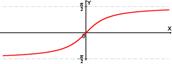
Функция y=arcsinX, её свойства и графики.

Арксинусом числа m называется такой угол x , для которогоФункция y = sinx непрерывна и ограничена на всей своей числовой прямой. Функция y = arcsinx является строго возрастающей. (функция является нечётной).

Функция y=arccosX, её свойства и графики.

Арккосинусом числа m называется такой угол x , для которого

Функция y = cosx непрерывна и ограничена на всей своей числовой прямой. Функция y = arccosx является строго убывающей. cos (arccosx ) = x при arccos (cosy ) = y при D (arccosx ) = [− 1; 1], (область определения), E (arccosx ) = [0; π]. (область значений). Свойства функции arccos (функция центрально-симметрична относительно точки

Функция y=arctgX, её свойства и графики.

Арктангенсом числа m называется такой угол α, для которого Функция непрерывна и ограничена на всей своей числовой прямой. Функция является строго возрастающей.

при

при

Свойства функции arctg

,

.