Шпаргалка: Лекции переходящие в шпоры Алгебра и геометрия

отсюда вытекает, что

порядок суммирования в двойной сумме можно менять.

Матрица

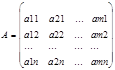
называется транспонированной по отношению к м-це А=

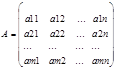
Обозначается А^Т . При транспонировании строки переходят в столбцы, а столбцы в строки и если А размером mxn, то А^Т будет размером nxm

Св-ва операции транспонирования.

1 (А^Т )^Т =А

2 (А+В)^Т =А^Т +В^Т

3 (СА)^Т =СА^Т (С-число)

4 (АВ)^Т =А^Т ×В^Т

4.Элементарные преобразования матрицы.

1 Переставление двух строк

2 Умножение строки на не равное 0 число В

3 Прибавление к строке матрицы другой ее строки, умноженной на число С.

Также производят элементарные преобразования столбцов.

5.Матрицы элементарных преобразований.

С элементарными преобразованиями тесно связаны квадратные матрицы элементарных преобразований. Они бывают следующих типов:

1 м-цы получающиеся из единичных путем перестановки двух любых строк например м-ца:

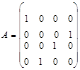получена перестановкой 2 и 4 строки

2 тип. м-цы получающиеся из единичной заменой диагонального элемента на произвольное не нулевое число:

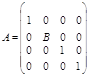
отличается от единичной элементом В во второй строке

3 тип отличающиеся лишь одним недиагональным не нулевым элементом: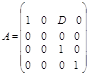

Основное св-во матриц элементарных преобразований Элементарное преобразование произвольной матрицы равносильно умножению этой м-цы на матрицу элементарных преобразований

Элементарные преобразования строк м-цы А

1 умножение м-цы А на м-цу 1 типа слева переставляет строки с номерами I,j

2 Умножение м-цы А на м-цу второго типа слева равносильно умножению j строки м-цы А на число В