Шпаргалка: Основы гидрогазодинамики

; ; ;

5. Основная теорема кинематики (первая теорема Гельмгольца)

Из теоретической механики известно, что скорость движения любой точки твердого тела складывается из поступательного вместе с некоторым полюсом и вращательного движения вокруг оси, проходящей через этот полюс: . Для жидкой частицы основная теорема кинематики гласит, что скорость движения любой точки жидкой частицы складывается из скорости квазитвердого движения и деформационного. Квазитвердое состоит из поступательного вращательного: . Для доказательства рассмотрим движение точки М с координатами x , y , z , которая находится в окрестности точки М₀ (x ₀ , y ₀ , z ₀ ) и составляющая для точки М₀ скорости ( u ₀ , υ ₀ , w ₀ ) , тогда раскладывая функцию скорости в ряд Тейлора и сохраняя компоненты первого порядка малости, составляющие скорости для точки М можно записать:

Преобразуем первое уравнение. Для этого разноименные части представим следующим образом:

;

- первая теорема Гельмгольца квазитвердое движение деформационное движение

6. Тензор скоростей деформации

Компоненты , входящие в скорость деформации, могут быть представлены в виде матрицы, которая называется тензором скоростей деформации:

- диагональные компоненты.

Тензор симметричен относительно главной диагонали

Рассмотрим диагональные компоненты. В жидкости выделим отрезок АВ длиной dx (отрезок на оси х ). Рассмотрим перемещение отрезка вдоль оси х . Скорости в точках А и В не равны. Через время dt отрезок займет положение . Произошла линейная деформация отрезка АВ на величину:

Если разделим линейную деформацию на длину отрезка:

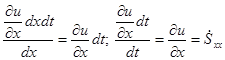
скорость линейной деформации – скорость растяжения или сжатия линейного отрезка расположенного на оси х в направлении оси х . Аналогично:

скорости относительных линейных деформаций вдоль соответствующих осей. Сумма диагональных компонент определяет дивергенцию вектора скорости, т.е.

закон относительного изменения объема.

Рассмотрим перемещение отрезка АВ расположенного на оси х и длиной dx в направлении оси dy ) .

Ввиду малости угла

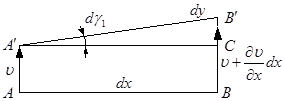
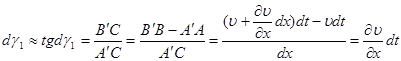
угловая деформация линейного отрезка в направлении оси у .

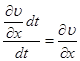
скорость угловой деформации или скорость скашивания в направлении оси у . Если отрезок расположить на оси у , то - скорость скашивания в направлении оси х . - средняя скорость угловой деформации в плоскости ху.