Шпаргалка: Основы гидрогазодинамики

7. Уравнение сплошности

Уравнение сплошности – это уравнение закона сохранения массы:

Выделим в жидкости элементарный объем с плотностью ρ.

Следовательно:

Второй член полученного уравнения выражает закон относительного изменения объема,. Т.е. дивергенцию.

Плотность в общем случае зависит от координат и времени:

Поэтому:

уравнение сплошности (неразрывности).

Если течение стационарное, то уравнение упрощается:

Если жидкость несжимаемая, т.е. , то

8. Нормальное и касательное напряжение, действующие в движущейся жидкости

Закон сохранения количества движения для неизолированной системы может быть записан в виде:

где - главный вектор количества движения системы

- главный вектор внешних сил, действующих на систему

В жидкости выделим элементарный тетраэдр с гранями , , , . Индекс показывает перпендикулярно какой оси расположены грани, - наклонная грань. К граням приложены соответствующие напряжения , , , (не перпендикулярные граням). Масса тетраэдра . На тетраэдр действуют массовые и поверхностные силы. Массовые характеризуются вектором плотности , поверхностные – напряжениями.

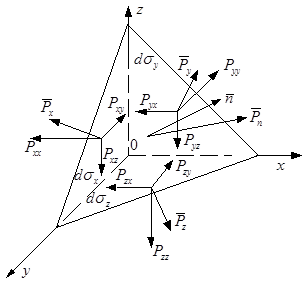
- скорость центра инерции тетраэдра

- третий порядок малости