Шпаргалка: Основы гидрогазодинамики

- система уравнений движения для и.ж. в форме Громека

Рассмотрим далее движение, предполагая, что массовая сила имеет потенциал и течение баротропное.

Первое предположение утверждает, что у массовых сил имеется потенциал, связанный соотношениями с массовыми силами:

; ; ,

U - потенциал массовых сил.

Второе: баротропным считается течение, у которого ρ считается только функцией давления.

Например, баротропными течением является:

1) ρ= const – газ или жидкость несжимаемы

2) движение среды изотермическое -

3) движение среды адиабатное -

Условие баротропности предполагает, что существует некоторая функция Р , зависящая от давления, которая определяется выражением:

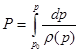
Функция Р связана с р и ρ соотношениями:

; ; .

Подставим в систему уравнений Громека потенциал массовых сил и функцию Р :

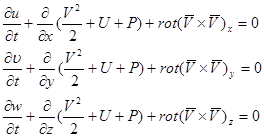
- система уравнений Эйлера в форме Громека

Достоинство системы заключается в том, что отдельно выделен ротор, который при определенных условиях может быть равен нулю и система значительно упрощается. Последний член равен нулю, если: 1) - статическая задача; 2) - течение безвихревое или потенциальное.

Сумма, стоящая во второй компоненте, имеет определенный физический смысл. В векторной форме система может быть записана в виде одного уравнения:

13. Теорема Бернулли

Рассмотрим стационарное баротропное течение под действием массовых сил, т.е. можно записать:

умножим уравнение скалярно на вектор скорости, тогда последний член равен нулю, т.к. идет скалярное перемножение перпендикулярных векторов.

- единичный вектор в направлении вектора скорости. Вектор скорости направлен по касательной к линии тока или к траектории, т.к. течение стационарное, следовательно:

- производная по направлению.