Шпаргалка: Шпаргалка по Математическому анализу

sin(α)=2tg(α/2)/(1+tg2(α/2))

cos(α)= (1-tg2(α/2))/ (1+ tg2(α/2))

sin(α)sin(β)=(1/2)(cos(α-β)-cos(α+β))

cos(α)cos(β)=(1/2)(cos(α-β)+cos(α+β))

sin(α)cos(β)=(1/2)(sin(α+β)+cos(α-β))

sin(α)-sin(β)=2sin((α-β)/2)cos((α+β)/2)

sin(α)+sin(β)=2sin((α+β)/2)cos((α-β)/2)

cos(α)+cos(β)=2cos((α+β)/2)cos((α-β)/2)

cos(α)-cos(β)=2sin((α+β)/2)sin((β- α )/2)

tg2(α)+1=1/cos2(α)

1+ctg2(α)=1/sin2(α)

2sin2(α)=1- cos2(α)

sin2(α)=(1- cos2(α))/2

Асимптоты .

Опр . Часть графика называется бесконечной ветвью если при движении точки по этой части, расстояние между ей и началом координат стремится к бесконечности.

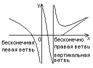
Опр. Прямая называется асимптотой бесконечной ветви графика функции, если при удалении точки от начала координат по этой ветви, расстояние до данной прямой стремится к нулю.

Теорема 1 : x=a (вертикальная прямая) – является асимптотой для бесконечно вертикальной ветви графика функции y=f(x), тогда когда f(x)®µ, при x®a.

Теорема 2 : Критерий существования наклонной асимптоты прямая y=kx+b является асимптотой для правой (левой) ветви графика функции тогда, когда существует предел при :

Док-во : Точка M0(x0,y0) и прямая

L: Ax+By+Cz=0, то расстояние

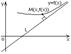Пусть y=kx+b

асимптота =>

d(M,l)®0=>

kx-f(x)+b®0

тогда f(x)-kx®b

при x®+µ

существует предел:

Дифференцирование функций заданных параметрически.