Учебное пособие: Математична обробка результатів вимірів
Похибка функції буде залежати від похибок її аргументів. Якщо виміряно аргументи Х1 , Х2 ..., Хn , то шляхом обчислень можна визначити функцію
де Х1 , Х2 ..., Хn - виміряні величини з середніми квадратичними похибками 
..., mxn . Припустимо, що нам відомі істинні похибки вимірів 
. Очевидно і функція отримає істинний приріст 
. Функція зведеться до вигляду
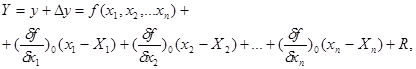
де 
- часткові похідні від функції по перемінних наближених значеннях аргументів;
xі —Хі = 
- істинні похибки аргументів функції;
R - величини другого та вищих порядків малості і в подальших розрахунках може бути прийнятою за нуль, тобто R=0.
Визначимо приріст функції 
у, для чого від рівняння віднімемо рівняння
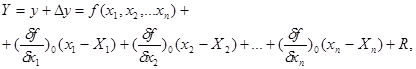
і отримаємо
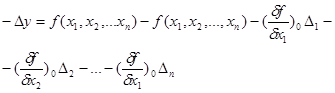
Для оцінки точності функцій застосуємо метод повторних вимірювань аргументів. Тобто припустимо, що аргументи функції виміряні n-разів і при відомих істинних похибках аргументів обчислено таку ж кількість похибок функції, тобто
, (i = l,n)
Зведемо їх до квадрата, складемо і поділимо на n. Отримаємо
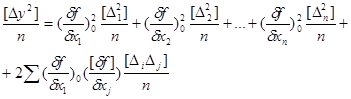
Із кореляційного аналізу можна визначити коефіцієнт кореляції за формулою
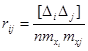
Тоді дисперсія функції зведеться до вигляду
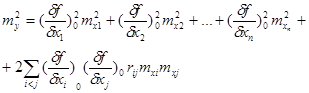
де 
- коефіцієнт кореляції, який виражає залежність між аргументами xi та xj .
Дві останні формули виражають дисперсію функції, тобто її точність залежно від виду функції і точності залежних між собою аргументів.
Практично досить важко і економічно невигідно визначати коефіцієнти кореляції. Тоді умовно приймають їх незалежними, а коефіцієнт кореляції rij = 0.
Для незалежних аргументів дисперсія функції буде
де my ,m1 , m2 , …, mn - середніквадратичніпохибкифункціїтаїїаргументів.
В узагальненому вигляді середню квадратичну похибку функції для незалежних аргументів виражають формулою
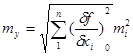
В теорії похибок вимірів для визначення дисперсії функції застосовують правило:
1. Диференціюють функцію