Учебное пособие: Моделирование электрических цепей в системе Mathcad

Подграфом графа называют часть графа. Подграфом может быть одна ветвь, узел или множество ветвей и узлов, содержащееся в данном графе.

Путь – упорядоченная последовательность ветвей, в которой каждые две соседние ветви имеют общий узел, причем любая ветвь и любой узел встречаются в этом пути только один раз (4–2–3).

Контур – замкнутый путь, в котором один из узлов является начальным и конечным узлом пути (1–2–4). На рис. 3.1 один из контуров содержит ветви 1, 2, 4.

Если между любой парой узлов графа существует путь, то граф называют связным.

Деревом связного графа называют связный подграф, содержащий все узлы графа, но не содержащий ни одного контура.

Примеры деревьев графа на рис. 3.1, б приведены на рис. 3.2:

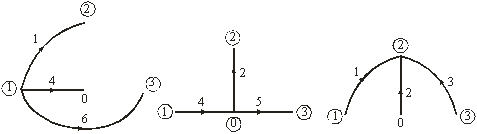
Рис. 3.2

Ветви графа, которые дополняют дерево до исходного графа, называют ветвями связи (хордами). Ветви графа, входящие в дерево, называют ребрами. Если граф содержит р ветвей и q узлов, то число ветвей любого дерева d = q - 1, а число ветвей связи k = p - q + 1.

Ветви связи деревьев графа на рис. 3.1, б приведены на рис. 3.3:

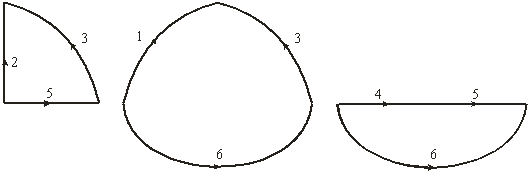
Рис. 3.3

Сечением графа называют множество ветвей, удаление которых делит граф на два изолированных подграфа, один из которых в частном случае может быть изолированным узлом.

Например, ветви графа 1–4–6, 3–2–4–6, 3–5–6 образуют сечения (рис. 3.4):

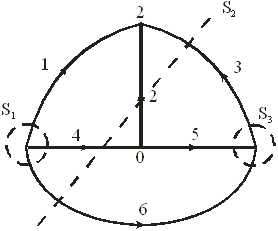
Рис. 3.4

Главным контуром называют контур, состоящий из ветвей дерева и только одной ветви связи. Другими словами, при соединении любой ветви связи с деревом образуется главный контур. Главным сечением считается сечение, состоящее из ветвей связи и только одной ветви дерева. Каждая ветвь дерева позволяет образовать одно сечение.

На рис. 3.5 показаны главные сечения, главные контуры для выделенного дерева графа (рис. 3.1, б):

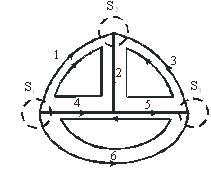
Рис. 3.5

3.2 Топологические матрицы графа

3.2.1 Матрица соединений

Матрица соединений (инциденций) А – это таблица коэффициентов уравнений, составленных по первому закону Кирхгофа (ЗКТ) для узлов.

Строки этой матрицы соответствуют узлам, столбцы – ветвям. Элементы а _ij матрицы А определяются следующим образом:

a_ij = 1, если ветвь j соединена с узлом i и направлена от узла;

a_ij = -1, если ветвь j соединена с узлом i и направлена к узлу;

a_ij =0, если ветвь j не соединена с узлом i .

Число строк матрицы А равно числу независимых узлов g = q - 1.

3.2.2 Матрица сечений

Матрица сечений D – это таблица коэффициентов уравнений, составленных по первому закону Кирхгофа (ЗКТ) для сечений. Строки матрицы D соответствуют сечениям, столбцы – ветвям.