Учебное пособие: Моделирование электрических цепей в системе Mathcad

– первый закон Кирхгофа (ЗКТ):

(3.9)

– второй закон Кирхгофа (ЗКН):

3.3 Полная система уравнений электрических цепей

Законы Кирхгофа применительно к графу схемы или электрической цепи характеризуют систему в целом без учета характеристик ее элементов. Матричные уравнения

Ai =- A Á (или Di =- D Á ) и Cu = Ce (3.10)

определяют систему из р отдельных уравнений. Такая система недостаточна для описания процессов в электрических цепях, так как не известны р токов и р напряжений.

Чтобы дополнить систему уравнений, необходимо определить (или задать) еще р уравнений. Эти уравнения должны отражать свойства элементов системы – ветвей электрической цепи. Очевидно, что такие связи должны быть записаны для р ветвей цепи. В матричной форме запишем эти уравнения в виде

i = f ( u ) или u = j ( i ),

т.е.

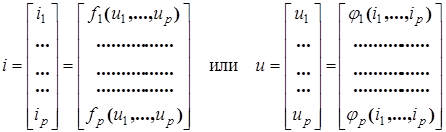(3.11)

В зависимости от характера функций f_k и j _k ( k =1…р) системы уравнений электрических цепей могут быть линейными – для линейных электрических цепей, т.е. для цепей, у которых r , L , С и М не зависят от значений и направлений токов и напряжений в цепи, и нелинейными – для нелинейных электрических цепей, т.е. для цепей, у которых r , L , С или М хотя бы одного из участков зависят от значений или от направлений токов и напряжений в этом участке цепи.

Каждая ветвь линейной цепи может содержать сопротивление, индуктивность, емкость, идеальный источник ЭДС и идеальный источник тока (рис. 3.9).

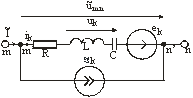
Рис. 3.9

Ток в сопротивлении ветви и падение напряжения ветви U связаны законом Ома.

U = Z × I ,

где сопротивление ветви 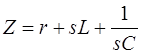. Эти соотношения для всех ветвей можно записать в матричной форме:

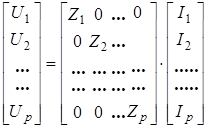
или кратко

U = Z × I , (3.12)

где Z – диагональная матрица сопротивлений ветвей;

U , I , J , E – соответственно векторы напряжений и токов ветвей, токов источников тока и ЭДС ветвей.

Это матричная форма закона Ома.

Замечание : Матрица Z диагональна лишь в случае, когда ток k -ой ветви создает напряжение на сопротивлении Z , k -ой ветви. В цепях со взаимной индукцией Z имеет элементы вне главной диагонали Z_ij = Z_ji = ± sM_ij .

М -сопротивления индуктивной связи i -ой и j - ой ветвей. Они положительны (отрицательны), если ориентация i -ой и j -ой ветвей по отношению одноименных зажимов одинакова (противоположна).

Уравнения закона Ома можно представить в другой форме:

I = Y × U , (3.13)