Учебное пособие: Основы теории вероятности

А={хотя бы одно попадание в цель при 4-х выстрелах}=0,9984

Решение

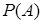=0,9984,

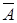= {ни одного попадания в цель при 4-х выстрелах}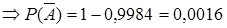

Вероятность непопадания при одном выстреле равна:

Окончательно получаем:

=

Задача №31. Студент обходит 3 библиотеки. Вероятность того, что книга есть в каждой из 3-х библиотек равна р₁ , вероятность того, что имеющаяся книга не выдана, равна р₂ . Какова вероятность того, что студент достанет книгу хотя бы в одной из библиотек.

Решение.

А₁ = {достанет книгу в 1-ой библиотеке};

А₂ = {достанет книгу во 2-ой библиотеке};

А₃ = {достанет книгу в 3-й библиотеке};

В₁ = {книга есть};

В₂ = {книга не выдана};

= {не достанет ни в одной библиотеке}.

– вероятность того, что студент достанет книгу хотя бы в одной библиотеке.

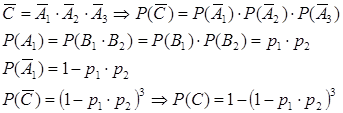
Задача №32. Охотник выстрелил 3 раза по удалённой цели. Вероятность попадания в цель в начале стрельбы равна 0,8. Вероятность попадания в цель после каждого выстрела уменьшается на 0,1. Найти вероятность попадания в цель 2 раза (событие D).

Решение. Пусть

A= {попадание в цель при 1-ом выстреле};

B= {попадание в цель при 2-ом выстреле};

C={попадание в цель при 3-ем выстреле}.

Тогда

P {A} = 0,8; P {B} = 0,7; P {С} = 0,6.

.

Задача №33. Вероятность того, что первый из 3-х человек придет, равна 0,8. Вероятность того, что второй придет, равна 0,4. Вероятность того, что придёт третий, равна 0,7. Найти вероятность того, что встреча состоится, если для этого нужно, чтобы пришли хотя бы двое из трёх.

Решение. Пусть

A={придёт первый};

B={придёт второй};

C={придёт третий};

D={придут хотя бы двое из трёх}.