Учебное пособие: Теория автоматического управления Структурная схема

D = 0.05Dx

Во время переходного процесса текущее значение отклонения управляемой величины может превышать установившееся отклонение. Разность между максимальным и установившимся отклонением, выраженная в процентах от установившегося отклонения, называется перерегулированием

|Dx_макс - Dx|

g = -------------------------------- 100%

|Dx|

Если переходная характеристика имеет колебательный характер, то оценивается так называемая колебательность.

Колебательность может быть определена отношением второго и первого максимумов переходной характеристики, выраженным в процентах

Dx_макс ,₂

G =------------------------ 100%

Dx_макс ,₁

Незатухающие колебания при этом соответствуют колебательности 100%. Колебательность стремится к нулю при уменьшении до нуля второго максимума переходной характеристики.

В данной курсовой работе переходная характеристика может быть получена экспериментально путем математического моделирования САУ (программа “CLASSIC”). При этом имеется возможность легко настраивать САУ на заданные качественные показатели изменением параметров, значения которых не заданы и могут варьироваться (например, Кос на рис.3.1). В качестве примера на рис.5.1 приведен вариант структурной схемы САУ рис.3.1, реализованной на компьютере при входном воздействии Df, выходном - Dx, Ку = 20, Кос = 20.

При исследовании переходного процесса в САУ, обусловленного изменением задающего воздействия (уставки) на DZ(рис.3.1) “вход” следует перенести на звено 4.

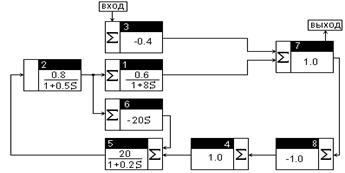
Рис.5.1. Вариант структурной схемы САУ рис.3.1.

Примечание. В программе “CLASSIC” оператор Лапласа обозначен S.

При исследовании переходной характеристики следует изменять параметры варьируемого звена САУ таким образом, чтобы характеристика по возможности имела монотонный характер без перерегулирования и колебательности. Если по каким-либо причинам этого достичь не удаётся, то можно считать допустимым

g£ 20 ¸ 25%; G £ 20%

На рис.5.2., 5.3. приведены переходные характеристики САУ рис.3.1 при Кос = 1.0; 10; 20 и Ку = 20 для воздействий Df и DZ соответственно.

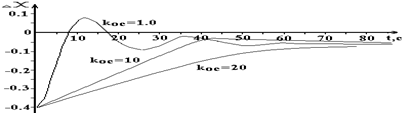
Koc = 1.0

t,c	0	2.06	4.1	6.2	8.2	10.3	11.33	14.42	20.6	23.69	34
Dx	-0.4	-0.35	-0.23	-0.09	0.013	0.072	0.083	0.057	-0,06	-0.08	-0.02

Koc = 10

t,c	0	4.7	7.8	10.9	14	20.2	26.4	29.5	35.7	42	45
Dx	-0.4	-0.37	-0.33	-0.29	-0.25	-0.16	-0.09	-0.07	-0.04	-0.02	-0.02

Koc = 20

t,c	0	4.6	9.13	15	20	25	29.6	38.7	47.8	59.2	68.3
Dx	-0.4	-0.38	-0.36	-0.3	-0.26	-0.23	-0.19	-0.14	-0.10	-0.07	-0.06

Рис.5.2. Переходная характеристика САУ рис.3.1 при входном воздействии Df(t) = 1.0 и различных значениях Koc.

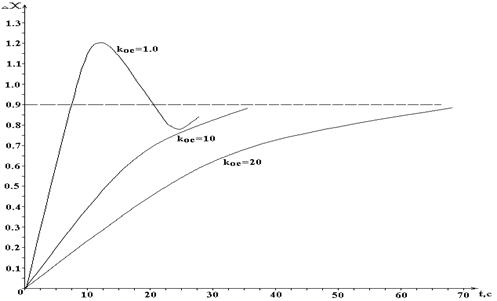
Koc = 1.0

t,c	0	2.25	4.5	6.2	9	10.1	11.3	11.8	13	14.6	18
Dx	0	0.154	0.49	0.77	1.1	1.17	1.21	1.21	1.19	1.13	0.95

Koc = 10

t,c	0	4	6	8	10	11	14	16	18.5	20.5	24.5
Dx	0	0.05	0.1	0.16	0.23	0.28	0.38	0.45	0.54	0.6	0.7

Koc = 20

t,c	0	4.4	10.3	14.7	19	23.5	29	38	45.5	48.4	57
Dx	0	0.3	0.13	0.22	0.31	0.4	0.51	0.64	0.71	0.74	0.8

Рис.5.3. Переходная характеристика САУ рис.3.1 при входном воздействии DZ = 1.0, Ку = 20 и различных значениях Koc.