Учебное пособие: Теория и методика обучения математике

Некоторые теоремы отражают свойства объекта (эти понятия), а некоторые его признаки.

Свойства понятия- это то что можем сказать о данном понятие всесторонне рассматривая его.

Признак понятия- это те показатели, по которым можно узнать данное понятие.

Отличить теорему выражающая свойство понятия от теоремы, выражающей его признаки помогает условная формы теоремы, если об объекте идет речь в условии, то это свойство понятия, а если в заключении, то признак, причем объект в формулировке встречается один раз.

П-р: Теорема: «Вокруг любого прямоугольника можно описать окружность.»- это свойство прямоугольника.

Теорема в условной форме выражается так «если параллелограмм является прямоугольником, то вокруг него можно окружность». Здесь идет речь в условии теоремы.

Теорема: «Параллелограмм, у которого диагонали равны, является прямоугольником»- это признак прямоугольника

Теорема в условной форме: «если диагонали параллелограмма равны, то он является прямоугольником».

Лекция 2. Индукция. Дедукция. Аналогия

Доказательство любой теоремы состоит из цепочки умозаключения.

Умозаключение- это рассуждение, в ходе которого из одного или нескольких суждений называемых посылками умозаключения выводятся новые суждения называемые заключением или следствием, логически вытекающих из посылок.

Умозаключение делится на непосредственные и опосредованные.

Непосредственным умозаключением называется умозаключение, если вывод делается на основании только одной посылки. (Н-р: параллелограмм- это четырехугольник.- нет не может)

Опосредованным умозаключением называется, если вывод делается на основании нескольких посылок. Умозаключение бывает достоверным, если вывод истинное утверждение и вероятностным, если истинность вывода не определена.

В зависимости от общности посылок и вывода выделяют следующие виды умозаключений:

Дедуктивное

Индуктивное

Традуктивное

Дедуктивное умозаключение или дедукция (от лат. выведение)- умозаключение от общего к частному, частичному или от более общего к менее общему.

Индуктивное умозаключение или индукция (от лат. наведение)- от частного к общему или от менее общего к более общему.

Традуктивное или традукция (от лат. перемещение)- умозаключение, в котором посылки и вывод имеют одинаковую степень общности.

Дедуктивное умозаключение - может быть непосредственным и опосредованным.

Самым распространенным видом опосредованного умозаключения является силлогизм.

В силлогизме содержатся три понятия, и состоит из посылок и вывода, его структуру можно представить в следующем виде:

Пример силлогизма

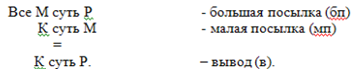
П - р силлогизма: Все ромбы (М) есть параллелограммы (Р).

Доказательство любой теоремы состоит из нескольких силлогизмов, на которые при доказательстве теорем делают ссылки только в устной форме, особо не выделяя силлогизмы (этапы доказательства).