Учебное пособие: Традиционные методы вычислительной томографии
Рассмотрим вначале физический закон распространения внешнего излучения в веществе. Пусть тонкий пучок, например ![]() - излучения, с интенсивностью
- излучения, с интенсивностью ![]() падает на слой вещества с распределением линейного коэффициента поглощения (ослабления)
падает на слой вещества с распределением линейного коэффициента поглощения (ослабления) ![]() вдоль распространения пучка. При этом феноменологически
вдоль распространения пучка. При этом феноменологически ![]() определяют через вероятность
определяют через вероятность ![]() поглощения
поглощения ![]() - кванта при прохождении элементарного пути
- кванта при прохождении элементарного пути ![]() соотношением
соотношением ![]() .
.
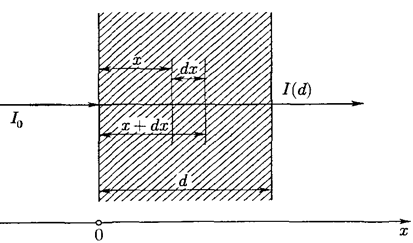 |
![]() Рисунок 1. К выводу уравнения переноса излучения (1.1).
Рисунок 1. К выводу уравнения переноса излучения (1.1).
Стационарное уравнение переноса излучения в чисто поглощающей неоднородной среде, описывающее процесс излучения в веществе, представляет собой баланс частиц или энергии и имеет вид
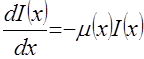 (1.1)
(1.1)
Решением уравнения (2.1) будет закон Бугера-Ламберта-Бэра для неоднородной поглощающей среды, который составляет основу расчетов ТВТ.
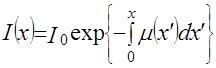 , (1.2)
, (1.2)
где ![]() - интенсивность источника излучения.
- интенсивность источника излучения.
Рассмотрим теперь закон распространения излучения при действии внутренних источников излучения (самоизлучающие объекты).
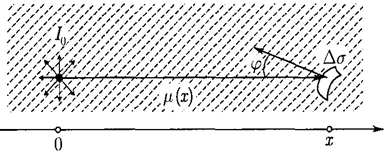 |
Рисунок 2. К выводу закона переноса излучения при действии внутреннего источника.
Пусть точечный источник излучает в телесный угол ![]() с интенсивностью
с интенсивностью ![]() в веществе с распределением линейного коэффициента ослабления
в веществе с распределением линейного коэффициента ослабления ![]() вдоль прямой, соединяющей источник с небольшой площадкой
вдоль прямой, соединяющей источник с небольшой площадкой ![]() , наклоненной под углом
, наклоненной под углом ![]() к этой прямой. Тогда для интенсивности
к этой прямой. Тогда для интенсивности ![]() , приходящейся на площадку
, приходящейся на площадку ![]() , получаем [3]
, получаем [3]
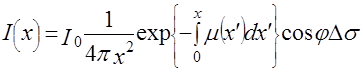 . (1.3)
. (1.3)
Выражение (1.3) учитывает четыре основных фактора: пространственное распределение источника излучения, геометрическое ослабление, ослабление излучения в веществе и наклон площадки детектора. Формула (1.3) лежит в основе ЭВТ.
2. ПРЕОБРАЗОВАНИЕ РАДОНА
2.1 Рассмотрим задачу восстановления двумерного распределения коэффициента ослабления ![]() при просвечивании объекта излучением внешнего источника. Источник излучения проходит дискретно вдоль объекта. Синхронно с источником с другой стороны объекта движется детектор излучения. Набор отсчетов, полученный таким образом, определяет одномерную функцию, называемую проекцией. Затем система «Источник-детектор» поворачивается относительно объекта на некоторый угол
при просвечивании объекта излучением внешнего источника. Источник излучения проходит дискретно вдоль объекта. Синхронно с источником с другой стороны объекта движется детектор излучения. Набор отсчетов, полученный таким образом, определяет одномерную функцию, называемую проекцией. Затем система «Источник-детектор» поворачивается относительно объекта на некоторый угол ![]() , и снимает новый набор отсчетов, определяющий следующую проекцию. По полученному набору одномерных проекций необходимо восстановить двумерное распределение
, и снимает новый набор отсчетов, определяющий следующую проекцию. По полученному набору одномерных проекций необходимо восстановить двумерное распределение ![]() . Такую схему измерений называют круговой геометрией измерений, а проекции называют параллельными проекциями.
. Такую схему измерений называют круговой геометрией измерений, а проекции называют параллельными проекциями.
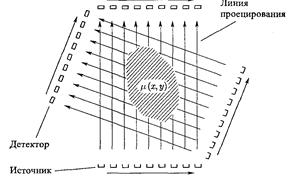 |
Рисунок 3. Схема кругового сканирования с параллельными проекциями.
Пусть на плоскости, где введена прямоугольная система координат ![]() задана функция
задана функция ![]() . Проинтегрируем эту функцию по некоторой прямой, лежащей в данной плоскости. Очевидно, что результат интегрирования, который обозначим
. Проинтегрируем эту функцию по некоторой прямой, лежащей в данной плоскости. Очевидно, что результат интегрирования, который обозначим ![]() , зависит от того, по какой именно прямой проводится интегрирование.
, зависит от того, по какой именно прямой проводится интегрирование.
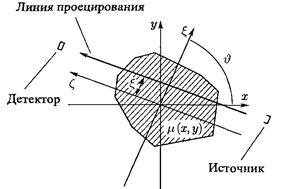 |
Рисунок 4. К выводу формул преобразования Радона.
Известно, что всякая прямая может быть описана уравнением
![]() , (2.1)
, (2.1)
где ![]() - расстояние от начала координат до этой прямой;
- расстояние от начала координат до этой прямой; ![]() - угол, образованный с осью
- угол, образованный с осью ![]() перпендикуляром, опущенным из начала координат на эту прямую.
перпендикуляром, опущенным из начала координат на эту прямую.
Произвольная прямая ![]() однозначно задается двумя параметрами
однозначно задается двумя параметрами ![]() и
и ![]() . Поэтому и результат интегрирования функции
. Поэтому и результат интегрирования функции ![]() по некоторой прямой будет зависеть от этих же параметров, т.е.
по некоторой прямой будет зависеть от этих же параметров, т.е. ![]() . Предположим, что функция
. Предположим, что функция ![]() интегрируется по всевозможным прямым. Подобное интегрирование можно также рассматривать как некоторое преобразование, которое данной функции
интегрируется по всевозможным прямым. Подобное интегрирование можно также рассматривать как некоторое преобразование, которое данной функции ![]() на плоскости
на плоскости ![]() ставит в соответствие функцию
ставит в соответствие функцию ![]() на множестве всех прямых, задаваемую интегралами от
на множестве всех прямых, задаваемую интегралами от ![]() вдоль прямых. Это преобразование называют преобразованием Радона [4,5], а функцию
вдоль прямых. Это преобразование называют преобразованием Радона [4,5], а функцию ![]() часто называют образом функции
часто называют образом функции ![]() в пространстве Радона или проекцией, которая в обозначениях (1.2) имеет вид
в пространстве Радона или проекцией, которая в обозначениях (1.2) имеет вид
 . (2.2)
. (2.2)
Задача ставится следующим образом: функция ![]() неизвестна, но известна функция
неизвестна, но известна функция ![]() , являющаяся образом
, являющаяся образом ![]() в пространстве Радона; требуется по функции
в пространстве Радона; требуется по функции ![]() определить
определить ![]() . Другими словами решение поставленной задачи сводится к отысканию явной формулы обращения или к поиску преобразования, обратного преобразованию Радона. Впервые формула обращения была получена в статье Иоганна Радона, опубликованной в 1917 году в Трудах Саксонской академии наук. Однако эта работа была незаслуженно забыта и формула обращения была открыта заново в 1961 году.
. Другими словами решение поставленной задачи сводится к отысканию явной формулы обращения или к поиску преобразования, обратного преобразованию Радона. Впервые формула обращения была получена в статье Иоганна Радона, опубликованной в 1917 году в Трудах Саксонской академии наук. Однако эта работа была незаслуженно забыта и формула обращения была открыта заново в 1961 году.
Согласно определению радоновского образа и с учетом того, что интеграл от заданной функции вдоль прямой равен интегралу по всей плоскости произведения этой функции на ![]() - функцию, аргументом которой является левая часть уравнения (2.3), имеем [6,7]
- функцию, аргументом которой является левая часть уравнения (2.3), имеем [6,7]
![]() . (2.3)
. (2.3)
Интегрирование, осуществляемое по двум переменным, можно свести к интегрированию по одной переменной. Для этого введем еще одну прямоугольную систему координат ![]() , повернутую относительно
, повернутую относительно ![]() на угол
на угол ![]() . Вспомним, что при переходе от одной из этих систем координат к другой координаты меняются следующим образом:
. Вспомним, что при переходе от одной из этих систем координат к другой координаты меняются следующим образом:
![]()
![]() (2.4)
(2.4)
![]()
![]() (2.5)
(2.5)
Сделаем в (2.3) замену переменных (2.4)