Учебное пособие: Традиционные методы вычислительной томографии

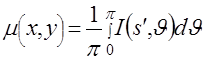, (2.28)

где при вычислении интеграла по величина должна быть заменена в соответствии с (2.26) на . В целом, алгоритм обращения преобразования Радона можно интерпретировать как последовательность операций:

1) для данного радоновского образа определяется его преобразование Фурье ;

2) функция умножается на ;

3) вычисляется обратное преобразование Фурье произведения и тем самым определяется функция ;

4) аргументу функции присваивается значение (2.26);

5) проводится интегрирование функции по углу .

Рассмотрим теперь иной вид формулы обращения по сравнению с (2.25). Обозначим через импульсную реакцию фильтра с частотной характеристикой . Связь между этими функциями устанавливается прямым и обратным преобразованием Фурье

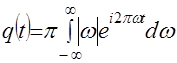(2.29)

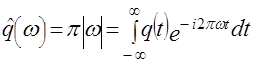(2.30)

Заметим, что функция обладает свойством .

Подставим в (2.25) вместо правую часть (2.30), а вместо - (2.17). Тогда получим

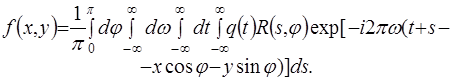
(2.31)

Интегрирование по дает , а последующее интегрирование по приводит к выражению

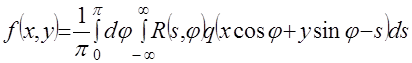(2.32)

Выражение (2.32) отличается от (2.25) тем, что в последнем участвует преобразование Фурье радоновского образа, а в (2.32) сам радоновский образ. Алгоритм (2.32) можно представить как совокупность трех последовательных операций:

1) вычисляется свертка данного радоновского образа с функцией ;

2) аргументу функции 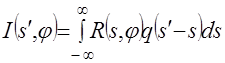, описывающей получаемую свертку, присваивается значение (2.26);

3) проводится интегрирование функции по углу .

2.5 Обращение экспоненциального преобразования Радона (2.14) – (2.16) представляет существенно более сложную задачу. Ограничимся здесь рассмотрением только случая радиально-симметричной функции . Тогда экспоненциальное преобразование Радона превращается в экспоненциальное преобразование Абеля [2]

==.

В [2] показано, что обратное экспоненциальное преобразование Абеля имеет вид

=

. (2.33)

3. МЕТОД РАЗЛОЖЕНИЯ В РЯД ФУРЬЕ (МЕТОД А. КОРМАКА)

В этом разделе рассмотрим восстановление функции изображения по ее проекциям, полученным при помощи внешнего источника излучения. Запишем искомую функцию в полярной системе координат . Тогда по переменной , , произвольная двумерная функция будет периодической и ее можно разложить в ряд Фурье

, . (3.1)

Аналогично разложим в ряд Фурье по переменной проекцию

, . (3.2)