Учебное пособие: Традиционные методы вычислительной томографии

Затем в равенство (4.1) вместо подставить найденные значения ,а в качестве использовать (4.3). При таких условиях последующее суммирование всех членов получившегося ряда позволяет реконструировать искомую функцию, так что

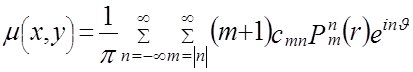, (4.6)

где и - полярные координаты в плоскости ,.

Чтобы разобраться, почему суммирование в (4.6) по индексу проводится от до, достаточно вспомнить, что все коэффициенты при равны нулю. Выбор полинома Чебышева приводит к тому, что коэффициенты обладают еще одним свойством: они также равны нулю, когда сумма их индексов является нечетной. Это следует непосредственно из формулы (4.5), если учесть два обстоятельства:

1) согласно (2.8) ;

2) полином Чебышева четного (нечетного) порядка является соответственно четной (нечетной) функцией своего аргумента.

Объединяя оба условия, имеем

, если или нечетно. (4.7)

Полезно также вспомнить, что для используемых полиномов Чебышева второго рода, которые определяются формулой

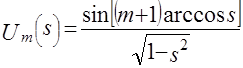, (4.8)

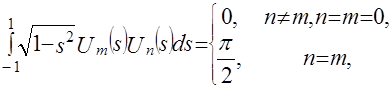(4.9)

так что эти полиномы ортогональны на отрезке [- 1, 1] относительно весовой функции .

Учитывая (4.9), можно показать [5], что

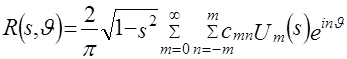. (4.10)

Сопоставляя (4.6) и (4.10), видим, что, как искомая функция , так и ее радоновский образ , выражаются через двойные суммы по индексам и , в которых используются одни и те же коэффициенты , но разные последовательности ортогональных функций.

Пример

Пусть , ее радоновский образ находится по (2.7) при и оказывается равным

.

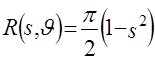Согласно (4.5), если то (из-за центральной симметрии функции), а для получаем значения коэффициентов разложения

=

=

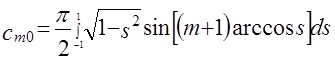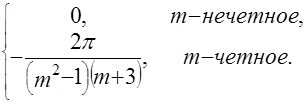
Выполняя суммирование в (4.6) с данными коэффициентами получим приближенное значение исходной функции изображения .

5. РЕГУЛЯРИЗАЦИЯ ФОРМУЛ ОБРАЩЕНИЯ

Обычно вместо точной проекции известна искаженная проекция

, (5.1)

где описывает соответствующую случайную погрешность,

проявляющуюся в данном случае в виде аддитивной добавки. Тогда задачу реконструкции можно переформулировать следующим образом: требуется по приближенным проекционным данным найти приближенную функцию , которая в каком-то смысле хорошо описывала бы искомую функцию . Непосредственная подстановка "зашумленных" проекционных данных [7] в указанный вычислительный алгоритм приводит к большим искажениям в . Дело в том, что задача реконструкции относится к так называемым некорректным задачам [8]. Физическая суть "некорректности" проявляется в том, что если пользоваться точным решением некорректной задачи, то даже при небольших искажениях в исходных данных это решение может существенно отличатся от искомой функции . Устранить это нежелательное явление можно, регуляризируя формулы обращения. В методах, основанных на преобразовании Радона (раздел 2) для этого достаточно "подавить" влияние высоких частот в , что можно, например, достичь умножением на регуляризующие функции . Обычно регуляризующие функции выбирают в следующем виде:

; (5.2)

; (5.3)