Учебное пособие: Традиционные методы вычислительной томографии

, (3.3)

Далее найдем гармонику

=

=, (3.4)

где . Преобразуем функцию , используя свойство - функции от сложного аргумента

,

где - функция Хевисайда, , . Следовательно,

, =

= (3.5)

где - многочлен Чебышева 1-го рода порядка . Выражение (3.5) представляет собой интегральное уравнение относительно неизвестной функции . В [3] показано, что решение (3.5) имеет вид:

. (3.6)

Итак, зная проекции , можно по формуле (3.2) найти гармоники , а затем вычислить гармоники по формуле (3.6) и, подставляя их в (3.1), найти искомую функцию .

Для радиально-симметричной функции в полярной системе координат преобразование Радона превращается в частный случай преобразования Абеля

= =

=. (3.7)

В [3] показано, что решение интегрального уравнения (3.7) имеет вид

. (3.8)

4. РЕКОНСТРУКЦИЯ ТОМОГРАФИЧЕСКИХ ИЗОБРАЖЕНИЙ ПРИ АППРОКСИМАЦИИ ПРОЕКЦИЙ ОРТОГОНАЛЬНЫМИ ПОЛИНОМАМИ

4.1. Рассмотрим алгоритм реконструкции изображения, основанный на приближенном представлении проекционных данных в виде конечного ряда ортогональных полиномов. Пусть имеется полная ортонормированная последовательность функций . Тогда, если искомая функция квадратично интегрируема, то она может быть представлена в виде
, (4.1)
где

, (4.2)

а - действительная неотрицательная весовая функция, относительно которой функции в области задания взаимно ортогональны.

Учитывая равенство (5.1), задачу реконструкции функции по ее радоновскому образу можно сформулировать как задачу нахождения коэффициентов по получаемым проекционным данным. Формально это означает, что требуется найти соотношение, например, типа (4.2), но которое определялось бы не функцией , а .Вид искомого соотношения зависит от конкретной ортогональной последовательности и определить его в общем случае не удается. В [5] приводится решение данной задачи для ортогонального базиса, составленного из функций

, (4.3)

где - полиномы Цернике, для которых выполняютсясоотношения

,

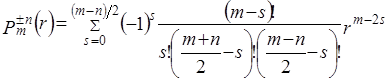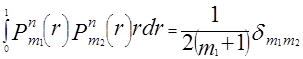. (4.4)

Опуская громоздкие промежуточные выкладки, приведем окончательные выражения и сопроводим их необходимыми пояснениями, вскрывающими их физическую сущность. Предварительно заметим, что если изучаемая функция задана в некоторой ограниченной области , то всегда эту область можно охватить окружностью с некоторым минимальным радиусом а , и, положив в тех точках ,,где соответствующий круг не пересекается с , рассматривать задачу о восстановлении функции в пределах данной окружности. Далее, произведя нормировку координат ,на величину , можно перейти к случаю восстановления функции в пределах окружности единичного радиуса. Лишь при выполнении данного условия возможно использовать последовательность функций (4.3).

Для реконструкции функции заданной в круге единичного радиуса, нужно по полученным проекционным данным рассчитать величины

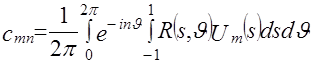, (4.5)