Учебное пособие: Традиционные методы вычислительной томографии
 . (2.16)
. (2.16)
2.3 Выражения (2.3), (2.6) позволяет по функции ![]() найти ее радоновский образ
найти ее радоновский образ ![]() . Существует соотношение, определяющее аналогичную связь между преобразованием Фурье этих функций. Пусть
. Существует соотношение, определяющее аналогичную связь между преобразованием Фурье этих функций. Пусть ![]() - одномерное преобразование Фурье функции
- одномерное преобразование Фурье функции ![]() по переменной
по переменной ![]() , а
, а ![]() - двумерное преобразование Фурье функции
- двумерное преобразование Фурье функции ![]() по переменным
по переменным ![]() . Согласно определению
. Согласно определению
 , (2.17)
, (2.17)
![]() . (2.18)
. (2.18)
В трехмерном пространстве введем прямоугольную систему координат, у которой по одной оси отложены значения ![]() , а по двум другим – значения
, а по двум другим – значения ![]() и
и ![]() .
.
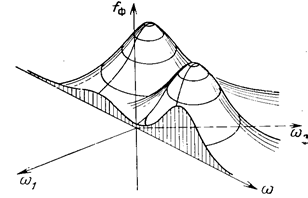 |
Рисунок 9. Центральное сечение двумерного преобразования Фурье
Проведем плоскость, перпендикулярную плоскости ![]() и проходящую через начало координат, такую, что линия ее пересечения с плоскостью
и проходящую через начало координат, такую, что линия ее пересечения с плоскостью ![]() составляет с осью
составляет с осью ![]() угол, равный
угол, равный ![]() (центральное сечение двумерного преобразования Фурье). В сечении этой плоскости со значениями функции
(центральное сечение двумерного преобразования Фурье). В сечении этой плоскости со значениями функции ![]() получается некоторая одномерная функция, зависящая от положения точки на этой прямой, например от ее расстояния до начала координат. Если это расстояние равно
получается некоторая одномерная функция, зависящая от положения точки на этой прямой, например от ее расстояния до начала координат. Если это расстояние равно ![]() , координаты точки этой прямой в плоскости
, координаты точки этой прямой в плоскости ![]() равны
равны ![]() и
и ![]() . Следовательно,
. Следовательно, ![]() подстановкой
подстановкой ![]() ,
, ![]() превращается в
превращается в ![]() .
.
Теорема.
Пусть функция ![]() и ее радоновский образ
и ее радоновский образ ![]() таковы, что существуют их преобразования Фурье. Тогда одномерное преобразование Фурье радоновского образа
таковы, что существуют их преобразования Фурье. Тогда одномерное преобразование Фурье радоновского образа ![]() по переменной
по переменной ![]() равно функции, описывающей центральное сечение двумерного преобразования Фурье, соответствующее тому значению
равно функции, описывающей центральное сечение двумерного преобразования Фурье, соответствующее тому значению ![]() , при котором вычисляется преобразование Фурье функции
, при котором вычисляется преобразование Фурье функции ![]()
![]() . (2.19)
. (2.19)
Для доказательства (2.19) подставим в (2.17) вместо ![]() выражение (2.6) и сделаем замену переменных, аналогичную (2.4), полагая в (2.4)
выражение (2.6) и сделаем замену переменных, аналогичную (2.4), полагая в (2.4) ![]() . Тогда получаем
. Тогда получаем
![]() =
=
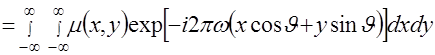 . (2.20)
. (2.20)
Сравнивая последний интеграл в (2.20) с (2.18), видим, что они равны, если в (2.20) под ![]() и
и ![]() понимать соответственно
понимать соответственно ![]() и
и ![]() . Следовательно, последний интеграл в (2.20) равен
. Следовательно, последний интеграл в (2.20) равен ![]() , что и доказывает сформулированную теорему. Легко убедиться, что теорема о центральном сечении справедлива и для случая, когда верно равенство (2.7).
, что и доказывает сформулированную теорему. Легко убедиться, что теорема о центральном сечении справедлива и для случая, когда верно равенство (2.7).
2.4 Рассмотрим теперь формулы обращения и алгоритмы реконструкции, основанные на теореме о центральном сечении. Известно, что по двумерному преобразованию Фурье ![]() можно найти
можно найти ![]() :
:
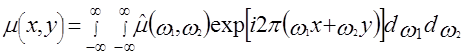 . (2.21)
. (2.21)
Сделаем в (2.21) замену переменных, перейдя в плоскости ![]() к полярным координатам
к полярным координатам ![]() , так что
, так что ![]() ,
, ![]() . Тогда (2.21) принимает вид:
. Тогда (2.21) принимает вид:
![]() . (2.22)
. (2.22)
Теперь воспользуемся равенством (2.19) и вместо ![]() подставим в (2.22) функцию
подставим в (2.22) функцию ![]() , после чего получим
, после чего получим
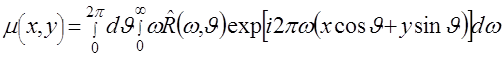 (2.23)
(2.23)
Равенство (2.23) и является искомой формулой обращения, позволяющей с учетом (2.17) по ![]() найти функцию
найти функцию ![]() . Однако привлечение этого равенства для обработки данных томографических экспериментов оказывается не очень удобным из-за используемой в нем области интегрирования. Принимая во внимание равенство
. Однако привлечение этого равенства для обработки данных томографических экспериментов оказывается не очень удобным из-за используемой в нем области интегрирования. Принимая во внимание равенство
![]() , (2.24)
, (2.24)
получим окончательное выражение для обращения преобразования Радона (см. Приложение Б)
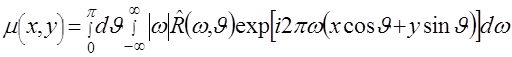 . (2.25)
. (2.25)
Для выявления детальной структуры алгоритма восстановления перепишем
(2.25) в несколько ином виде. Обозначим
![]() (2.26)
(2.26)
и введем функцию от ![]() и
и ![]() равную
равную
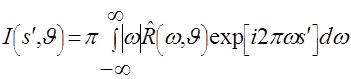 . (2.27)
. (2.27)