Дипломная работа: Качественное исследование в целом двумерной квадратичной стационарной системы с двумя частными интегралами в виде кривых второго и первого порядков
А.И. Яблонский [8, c. 1752] и В.Ф. Филипцов [9, c. 469] изучали квадратичные системы с предположением, что частными интегралом являлись алгебраические кривые четвёртого порядка.
В данной работе рассматривается система:
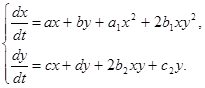
и проводится качественное исследование в целом этой системы при условии, что её частными интегралами являются две кривые–первого и второго порядков. Качественное исследование включает в себя нахождение и исследование состояний равновесия, а также определение направлений траекторий в состоянии равновесия, исследование бесконечно-удалённой части плоскости и качественная картина для построенных систем.
При определённых ограничениях на коэффициенты системы и интегралов строятся классы дифференциальных систем с заданными интегралами, при этом коэффициенты интегралов выражаются через коэффициенты системы, а коэффициенты системы связаны между собой соотношениями.
Работа состоит из двух разделов.
В первом разделе проводится построение квадратичных двумерных стационарных систем с заданными интегралами.
Во втором разделе проводится качественное исследование в целом выделенных в первом разделе классов систем при фиксированных значениях некоторых параметров.
1. Построение квадратичной двумерной стационарной системы
1.1 Построение квадратичной двумерной стационарной системы с частным интегралом в виде кривой второго порядка
Рассмотрим систему дифференциальных уравнений:
![]()
![]()
![]()
![]()
В данной работе будем рассматривать систему, в случае когда с1 =а2 =0 , то есть систему:
![]()
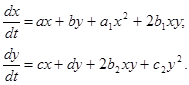 (1.1)
(1.1)
Пусть система (1.1) в качестве частного интеграла имеет интеграл вида:
![]()
![]()
![]() (1.2)
(1.2)
![]()
где Fk (x, y) – однородный полином от x и y степени k.
В качестве частного интеграла (1.2) возьмём кривую второго порядка вида:
F ( x , y )= y 2 + αxy + βx 2 + γy +δ x +σ=0 . (1.3)
Согласно [8, c. 1752–1760] для интеграла (1.3) системы (1.1) имеет место соотношение:
![]() (1.4)
(1.4)
где L ( x , y )= mx + ny + p , m , n , p -постоянные.
Тогда для частного интеграла (1.3) получим равенство:
( α y+2βx+δ) (ax+by+a1 x2 +2b1 xy)+(2y+αx+γ) (cx+dy+2xy+c2 y2 )=
(y2 +αxy+βx2 +γy+δx+σ) (mx+ny+k).
Будем предполагать, что коэффициенты системы (1.1) b 1 = b 2 = c 2 =1 , тогда для интеграла (1.3) получим равенство:
(α y +2 βx + δ ) ( ax + by +а1 x 2 +2 xy )+(2 y + αx + γ ) ( cx + dy +2 xy + y 2 )=