Дипломная работа: Кручение стержней

ОГЛАВЛЕНИЕ

Введение

Глава 1. Кручение стержней имеющих в сечении правильный многоугольник

§1.1 Кручение призматических стержней

§1.2 Кручение стержней прямоугольного сечения

§1.3 Мембранная аналогия

§1.4 Кручение тонкостенных стержней открытого профиля

Глава 2. Кручение стержней имеющих в сечении круг и эллипс

§2.1 Кручение стержней круглого и эллиптического сечений

§2.2 Кручение тонкостенных труб

§2.3 Кручение круглых валов переменного диаметра

Глава 3. Кручение призматических и цилиндрических стержней

§3.1 Чистое кручение стержней постоянного сечения

§3.2 Чистое кручение круглых стержней (валов) переменного сечения

Глава 4. Задачи

Заключение

Литература

ВВЕДЕНИЕ

Данная выпускная квалификационная работа состоит из четырех глав. В первой главе излагается прямой, обратный и полуобратный методы, применяемые при решении задач о кручении стержня прямоугольного сечения. Исследованы приближенные методы решения задач о кручении более сложных сечений.

Вторая глава посвящена изучению кручения стержней в сечении имеющих форму круга или эллипса. Применяют метод перехода к полярным координатам.

В третьей главе исследуется кручение призматических и цилиндрических стержней, исследуются общие построения данной теории и их различия.

В четвертой главе изучают теоретическое применение к решению задач.

Глава 1. КРУЧЕНИЕ СТЕРЖНЕЙ, ИМЕЮЩИХ В СЕЧЕНИИ ПРАВИЛЬНЫЙ МНОГОУГОЛЬНИК

§1.1 Кручение призматических стержней

Прямой метод решения задач теории упругости, заключающийся в интегрировании основных уравнений теории упругости совместно с заданными граничными условиями, не всегда возможен. Для многих задач удобно применять так называемые обратный и полуобратный методы. При пользовании обратным методом выясняют, каким граничным условиям соответствуют некоторые функции, удовлетворяющие дифференциальным уравнениям. Таким путем можно получить ряд полезных результатов. Полуобратный метод, впервые предложенный Сен-Венаном, состоит в том, что делают некоторые допущения в отношении напряжений или перемещений. При этом дифференциальные уравнения настолько упрощаются, что решение их не представляет особых математических трудностей. Принимая те или иные допущения, мы, как правило, ограничиваем общность полученного решения; но обычно их можно формулировать таким образом, чтобы все же получить решение частных задач. Например, в рассматриваемой ниже задаче о кручении призматического стержня мы будем задаваться определенными функциями для перемещений и, v, w, сводя, таким образом, основные уравнения к одному дифференциальному уравнению. Но при таких допущениях мы можем найти решение задачи о кручении стержней только постоянного сечения; решения же для стержней, не являющихся призматическими, получить этим путем нельзя. Полуобратный метод является одним из самых эффективных методов решения задач теории упругости.

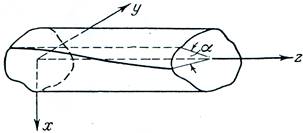
рис. 1

Предположим, что один конец стержня призматического сечения, длины L, закреплен в плоскости ху, а на другой конец действует пара, вектор-момент который направлен вдоль оси z (рис. 1). Мы полагаем, что закрепленный конец не может вращаться, но что оба конца могут свободно перемещаться друг относительно друга в направлении z. Под действием пары стержень будет закручиваться, причем образующие цилиндра будут превращаться в винтовые линии. Угол поворота любого поперечного сечения зависит от расстояния, на котором находится это сечение от закрепленного конца. При малой деформации можно считать, что угол закручивания пропорционален расстоянию между сечением и закрепленным концом. Таким образом,

z, (1)

--> ЧИТАТЬ ПОЛНОСТЬЮ <--