Дипломная работа: Кручение стержней

рис. 3

здесь принято

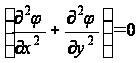
в соответствии с уравнением (6).

Пусть f является некоторой функцией x и y; тогда можно выписать равенства (рис. 3):

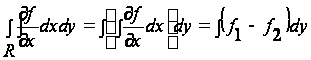
где f1 и f2 - значение функции f на правой и левой частях контура. Выполним интегрирование по y для контурной кривой в границах от y=yA до y=yB. Если мы будем вести интегрирование функции f по контуру в направлении против часовой стрелки, то для правой части контура приращение dy - положительно, а для левой - отрицательно. В результате каждая из величин f1dy и (- f2dy) окажется положительной, и, следовательно,

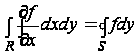. (10)

Аналогично,

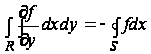(11)

Пользуясь формулами (10) и (11), придадим выражению (9) вид:

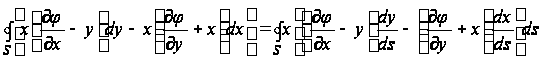. (12)

Будем считать положительными направления вдоль нормали N во внешнюю сторону и вдоль контура – против часовой стрелки; тогда согласно рис.3,б получим

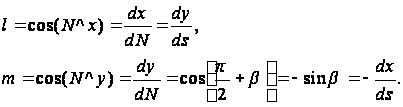(13)

Равенство (12) принимает вид

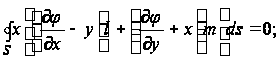
при этом выражение

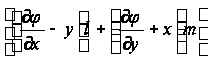
обращается в нуль на контуре S в соответствии с уравнением (7). Мы пришли, таким образом, к равенству

Таким же путем можно показать, что составляющая результирующей силы вдоль оси также равна нулю:

Следовательно, результирующие силы по торцам цилиндра обращаются в нуль.

Результирующий крутящий момент T по торцам стержня, отвечающий принятому распределению напряжений, равен:

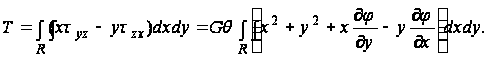(14)

Интеграл, фигурирующий в выражении (14), зависит от функции кручения и, следовательно, от вида поперечного сечения R стержня. Вводя обозначение

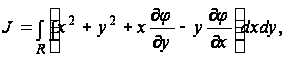(15)

Получим

(16)