Дипломная работа: Кручение стержней

Пользуясь аналогией, можем написать

.

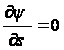Из соотношений

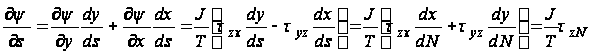
вытекает, что составляющая касательного напряжения, направленная по нормали к горизонтали, равна нулю. Другими словами, касательное напряжение в точке В закручиваемого стержня направлено по касательной по горизонтали, проходящей через эту точку. Величину результирующего касательного напряжения можно найти из следующей формулы:

.

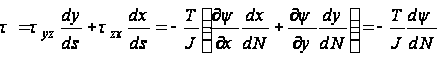Следовательно, величина касательного напряжения в точке В определяется уклоном мембраны по нормали к горизонтали, и потому касательные напряжения достигают максимума в тех местах, где горизонтали особенно сгущаются. Рассмотрение поверхности мембраны показывает, что наибольший уклон имеет место на контуре. Отсюда можно заключить, что максимальные значения касательных напряжений будут также в определенных точках контура сечения стержня.

Обратимся к выводу выражения для постоянной кручения J через функцию . Из формулы (15) имеем:

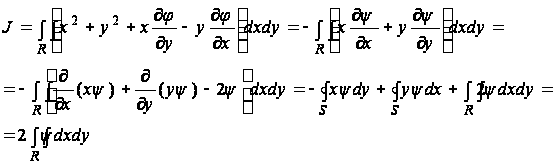(53)

Здесь использовано то обстоятельство, что по формуле (52) на контуре S будет . Из мембранной аналогии вытекает, что постоянная кручения J равна удвоенному объему, заключенному между изогнутой мембраной и плоскостью xy. Полагая c2=0, в (52) мы считали, что величина c2 не влияет на решение задачи. Однако значение J, на первый взгляд, зависит от величины c2. Чтобы выяснить это, допустим, что c2 и подставим вместо в последнее из выражений (53). Так как в точках контура , то для них ; следовательно, члены, содержащие контурные значения , будут равны нулю так же, как это для функции . Таким образом,

.

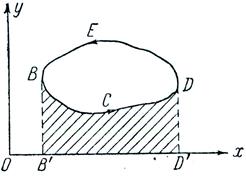
рис.11

Пользуясь, рис .11, приходим к соотношениям

площади BCDD’- площадь BEDD’= -A , (54)

где А - площадь поперечного сечения. Подобным же образом можно показать, что. Но в то же время . Следовательно,

,

что совпадает с формулой (53).

§1.4 Кручение тонкостенных стержней открытого профиля

Рассмотрим вначале кручение стержня с поперечным сечением в форме узкого прямоугольника. Из мембранной аналогии заключаем, что влияние коротких сторон прямоугольника распространяется на небольшие участки. Если отношение b/a велико, то в формуле (43) величину можно приближенно считать равной 1; второй член в скобках становится пренебрежимо мал. Поэтому имеем

.

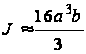Обратимся к формуле (45). При значительном отношении b/a величина

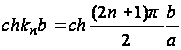
будет большой, сумма же бесконечного ряда получает пренебрежимо малое значение. В результате получаем

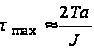. (55)

Если величина J известна, то угол закручивания можно вычислить по формуле

. (16)

Обозначим через b1 длину, а через t – толщину прямоугольника (рис.12,а); тогда эти формулы примут вид:

t. (56)