Дипломная работа: Кручение стержней

Касательные напряжения в некоторой точке поперечного сечения равны:

(27)

Результирующее касательное напряжение в точке P(x,y) равно

(28)

рис.4

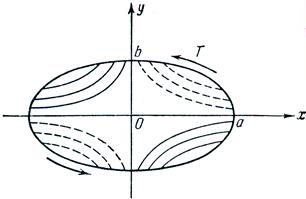
Напряжение достигает максимального значения на концах малой оси. Чтобы показать это, построим ряд эллипсов внутри сечения. Пусть полуоси эллипсов будут a’ и b’, причем .

Уравнения этих эллипсов могут быть записаны в параметрической форме следующем образом:

где угол, показанный на рис.4. Подставляя эти значения x и y в уравнение (28), получаем результирующие касательные напряжения в любой точке этих эллипсов:

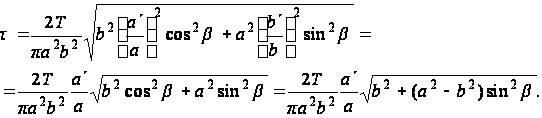
Если a > b, то будет максимально при a’= a и . Таким образом, касательное напряжение имеет максимум у концов малой оси, величина в этих точках равна:

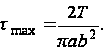(29)

При a = b эта формула переходит в выражение (21), относящееся к стержню круглого сечения. Направление напряжения определяется отношением величин и . Из формул (27) видно, что это отношение пропорционально отношению y/x и, следовательно, постоянно вдоль линии OP. Это означает, что результирующее касательное напряжение вдоль линии OP имеет постоянное направление, совпадающее с направлением касательной P’P".