Дипломная работа: Кручение стержней
§1.2 Кручение стержней прямоугольного сечения
Пусть поперечное сечение стержня представляет собой прямоугольник с центром в начале координат и со сторонами 2a и 2b, направленными параллельно координатным осям, как показано на рис.7. Пользуемся полученными ранее уравнениями: для всей прямоугольной области
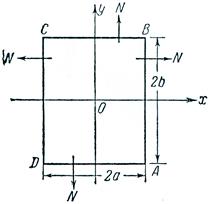
рис.7
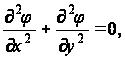 (6)
(6)
и по контору
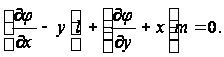 (7)
(7)
На контурных линиях AB и CD, где x=![]() a, будет l=
a, будет l=![]() 1 и m=0 , а на линиях BC и AD имеем l=0 и m=
1 и m=0 , а на линиях BC и AD имеем l=0 и m=![]() 1 . Условие на контуре (7) можно переписать в следующем виде:
1 . Условие на контуре (7) можно переписать в следующем виде:
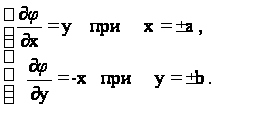 (31)
(31)
Этим условиям можно придать более удобную форму, вводя новую функцию ![]() так, что
так, что
![]() . (32)
. (32)
Легко показать, что для новой функции ![]() основное уравнение по всей прямоугольной области будет иметь вид:
основное уравнение по всей прямоугольной области будет иметь вид:
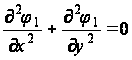 ; (33)
; (33)
условия на контуре будут следующими:
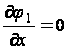 при
при ![]() (34)
(34)
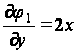 при
при ![]() (35)
(35)
Примем решение уравнения (33) в виде бесконечного ряда
 (36)
(36)
каждый член, которого удовлетворяет дифференциальному уравнению; здесь Xn(x) и Yn(y) – функции соответственно только x и y. Очевидно, если решение для ![]() нельзя выразить в форме ряда (36), то мы не сможем найти решение для функции Xn и Yn , удовлетворяющее граничным условиям.
нельзя выразить в форме ряда (36), то мы не сможем найти решение для функции Xn и Yn , удовлетворяющее граничным условиям.
Подставляя Xn(x), Yn(y) в уравнение (33) и обозначая производные штрихами, находим
![]()
Или

Так как левая часть полученного уравнения является функцией только от x, а правая зависит только от y, то уравнение может быть удовлетворено лишь в том случае, если обе его части равны постоянной величине; обозначим ее через (![]() ) (постоянную берем со знаком минус, так как иначе граничные условия не будут удовлетворяться). Таким образом, мы получаем два обыкновенных дифференциальных уравнения:
) (постоянную берем со знаком минус, так как иначе граничные условия не будут удовлетворяться). Таким образом, мы получаем два обыкновенных дифференциальных уравнения:

Эти дифференциальные уравнения легко решить с помощью известных методов интегрирования обыкновенных дифференциальных уравнений с постоянными коэффициентами. Решение их будут следующими:
![]() (37)
(37)
![]() (38)
(38)
Рассмотрим теперь условие на контуре (35). Во-первых, можно установить, что выражение