Дипломная работа: Кручение стержней

где K2 - второй числовой множитель, значения которого также даны в табл. 1.1.

Горизонтали поверхности, для которых , могут быть легко определены из уравнения для функции . Для стержня квадратного сечения, т.е. при a=b , горизонтали на рис.8; здесь сплошные линии соответствуют положительным значениям w, а пунктирные – отрицательным, по правилу знаков.

§1.3 Мембранная аналогия

Из примера, разобранного в предыдущем параграфе, становится очевидным, что задачи о кручении стержня более сложной формы поперечного сечения может оказаться весьма трудным. Для приближенного решения задач о кручения стержней различных сечений, часто встречающихся в технике, весьма эффективной оказались так называемая мембранная аналогия. Она основана на математической аналогии между задачами о кручении и о деформации упругой натянутой мембраны, подверженной равномерному поперечному давлению.

рис.9

Пусть тонкая однородная мембрана (рис.9) имеет постоянное натяжение и закреплена по контуру, который ограничивается кривой, лежащей в

плоскости xy. Если мембрана подвергается равномерному поперечному давлению p, то точки её срединной поверхности получат перемещения z, зависящие от x и y. Рассмотрим условие равновесия бесконечного малого элемента ABCD мембраны после деформации. Обозначим через F постоянное натяжение, приходящееся на единицу длины мембраны. Усилие F, действующее по стороне AD, наклонено к оси под углом . Так как деформации малы, то можно принять . Прогиб z меняется от точки к точке, поэтому усилие F для стороны BC наклонено под углом

.

Таким же путем находим, что углы наклона растягивающих усилий, приложенных по сторонам AB и CD, равны соответственно и .

Складывая составляющие вдоль оси сил, действующих по четырем сторонам, получаем

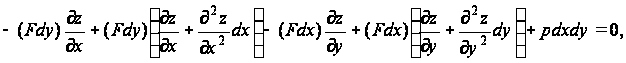
отсюда

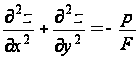… для области R. (47)

На контуре прогиб мембраны равен нулю. Поэтому граничное условие имеет вид:

z=0 на контуре S. (48)

Вернемся теперь к задаче о кручении. Основное дифференциальное уравнение будет:

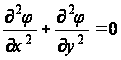для области R, (6)

а граничное условие имеет вид:

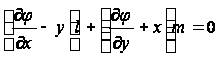на контуре S. (7)

На первый взгляд эти соотношения и уравнения (47) и (48) не являются аналогичными. Однако им можно придать идентичную форму, если ввести новую функцию с помощью соотношений:

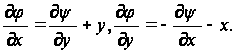(49)

Из уравнений (49) имеем

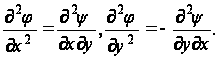
Дифференциальное уравнение (6) обращается в тождество, так как

+ =

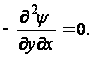
Таким образом, если функция определяется по формулам (49), то уравнения равновесия будут удовлетворяться тождественно.

Выражая касательные напряжения и через функцию , получаем

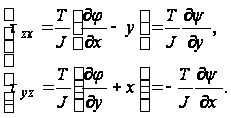(50)