Дипломная работа: Кручение стержней

рис.12

Сопоставим теперь изогнутые мембраны с контурами, изображенными на рис.12,а и б. Очевидно, что если площади поперечного сечения их равны между собой, то равными будут и объемы выпучен в изогнутых мембранах. Если толщина t мала, то кривизна сечения в случае (б) незначительно влияет на максимальный уклон мембраны. Поэтому мы делаем вывод, что формула (56) может быть использована при получении приближенных решений и для тонкостенных профилей иной формы. Для поперечных сечений такого типа, который показан на рис.12,б, надо только вместо b1 в формуле (56) подставить развернутую длину дуги. В случае дуги окружности развернутая длина равна , где радиус, а угол, стягиваемый дугой, в радианах.

Для таких тонкостенных профилей, как уголки, швеллера и двутавры,

вид изогнутых мембран будет таким, как если бы они были натянуты на несколько отдельных узких прямоугольников. Постоянная кручения J будет равна удвоенному объему, ограниченному изогнутой мембраной и плоскостью xy; максимальный уклон мембраны окажется равным , причем большая из величин ti или t2. Следовательно, для уголкового сечения имеем (рис.12, в):

(57)

а для швеллерного и двутаврового сечения (рис.12, г):

(58)

Следует заметить, что во входящих углах имеет место значительная концентрация напряжений, зависящая от радиуса закруглений углов профиля. Для малых радиусов закруглений (r=0.1t) Трефц получил следующее уравнение для максимальных напряжений в углах профиля:

(59)

где r - радиус закругления угла. Уравнение (59) выведено для случая полок равной толщины. Если же полки имеют различную толщину t1 и t2, то в формулу следует подставить большую из них. Концентрация напряжений во входящих углах изучалось экспериментально, причем была использована аналогия с мыльной пленкой. Отношения , соответствующие различным значениям отношения r/t, приведены в табл.1.2. Экспериментально полученные величины отношения для малых радиусов закругления ребер профиля значительно меньше вычисленных по формуле (59). Это, вероятно, можно объяснить тем, что при малых радиусах закруглений трудно определить истинные значения .

Таблица 1.2

				1
	2,5	2,25	2,00	1,75

ГЛАВА 2.КРУЧЕНИЕ СТЕРЖНЕЙ, ИМЕЮЩИХ В СЕЧЕНИИ ОКРУЖНОСТЬ ИЛИ ЭЛЛИПС

§2.1 Кручение стержней круглого и эллиптического сечений

Было показано, что для решения задачи о кручении надо найти функцию депланации , которая удовлетворяет дифференциальному уравнению

(6)

во всех точках поперечного сечения, т.е. в области R , и условию

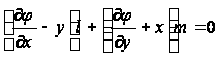(7)

на контуре S. Выясним, как найти решение для контура определенной формы.

Задача о кручении стержня круглого и эллиптического сечения решалась с помощью обратного метода. Простейшее решение уравнения Лапласа имеет вид:

(17)

При условие на контуре (7) записывается в следующем виде:

Отсюда

,

или

(18)

где x,y - координаты некоторой точки контура. Из аналитической геометрии известно, что уравнение (18) отвечает окружности с центром в начале координат. Таким образом, выбор функции в виде дает нам решение задачи о кручении стержня круглого сечения. Уравнение (3) дает . Примем граничное условие w=0 при z=0; тогда C=0. Следовательно, плоское сечение цилиндра, перпендикулярное к оси, до закручивания, остается плоским и после деформации. Такое допущение обычно делается при решении задачи методами сопротивления материалов. Но уравнение (18) показывает, что это предположение справедливо только в случае кругового контура; нельзя ожидать, что оно будет справедливым для сечений другой формы.