Дипломная работа: Порушення основних припущень лінійного регресійного аналізу

1.12 Лінійна регресія з двома незалежними змінними

РОЗДІЛ ІІ Дослідження порушень основних припущень лінійного регресійного аналізу

2.1 „Ідеальна” модель лінійної регресії

2.2 Модель лінійної регресії, в якій дисперсія спостережень величина змінна

2.3 Модель лінійної регресії, в якій спостереження величини залежні

2.4 Модель лінійної регресії, в якій спостереження рівномірно розподілені величини

2.5 Модель лінійної регресії, в якій спостереження показниково розподілені величини

ВИСНОВКИ

СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ

ВСТУП

Нехай – результат спостереження, який описується лінійною моделлю виду

(1)

де – регресійна матриця розміру , ,

– вектор невідомих параметрів,

– вектор похибок спостережень.

Припущення відносно вектора спостережень позначатимемо :

.(2)

Або, що те ж саме, припущення відносно вектора похибок мають вигляд:

(3)

Вихідні припущення (2) або (3) регресійного аналізу виконуються далеко не завжди. Виникає низка питань: як виявити порушення цих припущень? В яких випадках і які порушення можна вважати припустимими? Що робити, якщо порушення виявляються неприпустимими?

Метою роботи є вивчення наслідків порушення основних припущень (3) лінійного регресійного аналізу, а саме:

1) припущення про незміщеність похибок ;

2) припущення про однакову дисперсію і некорельованість похибок ;

3) припущення про нормальний розподіл похибок ;

4) припущення про незалежність спостережень .

РОЗДІЛ І П РОСТА ЛІНІЙНА РЕГРЕСІЯ

1.1 Постановка задачі

Нехай – вибірка, утворена незалежними нормально розподіленими випадковими величинами з однією і тією ж дисперсією і середніми, про які відомо, що вони лінійно залежать від параметрів, тобто мають вигляд

,(1.1.1)

де – відомі невипадкові величини; – невідомі параметри.

Кожну з випадкових величин можна подати у вигляді

, (1.1.2)

де називають похибкою спостережень. Похибка змінюється від спостереження до спостереження, () - незалежні випадкові величини. Відносно будемо припускати, що

1)

2) , некорельовані при

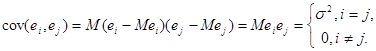
(з незалежності , випливає їх некорельованість)