Дипломная работа: Порушення основних припущень лінійного регресійного аналізу
, де 
Число ступенів вільності цієї суми 
.
Сума квадратів, пов’язана з “чистою помилкою” при 
дорівнює
, де 
Число ступенів вільності цієї суми 
і т. д.
Загальна сума квадратів, пов’язана з “чистою помилкою”дорівнює
з загальним числом ступенів вільності
Звідси середній квадрат для “чистої помилки” дорівнює
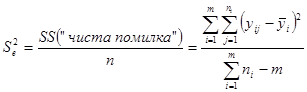(1.9.1)
і є оцінкою для 
.
Покажемо, що сума квадратів, пов’язана з “чистою помилкою”, є частиною суми квадратів залишків (суми квадратів відносно регресії).
Залишок для 
-того спостереження при 
можна записати у вигляді:
Піднесемо праву та ліву частини рівності до квадрату.
Візьмемо суму по кожному з індексів 
та .
(1.9.2)
при цьому 
.
Суму (1.9.2) можна записати так
Сума Сума квадратів Сума
квадратів = “чистих + квадратів (1.9.3.)
залишків помилок” неадекватності
Число ступенів вільності:
Отже, суму квадратів “чистих помилок” можна ввести в таблицю дисперсійного аналізу.
Таблиця 1.9.1. Таблиця дисперсійного аналізу
| Джерело варіації |
Число ступенів вільності |
Сума квадратів
|
К-во Просмотров: 331
Бесплатно скачать Дипломная работа: Порушення основних припущень лінійного регресійного аналізу
|
