Дипломная работа: Порушення основних припущень лінійного регресійного аналізу

Розглянемо суму квадратів, обумовлену регресією .

Єдиною функцією від є оцінка , оскільки, . Тому число ступенів вільності цієї суми квадратів дорівнює .

Число ступенів вільності суми квадратів дорівнює .

Отже, згідно з (1.3.3) ми можемо розкласти ступені вільності суми квадратів так:

(1.3.4)

За допомогою (1.3.3) та (1.3.4), побудуємо таблицю дисперсійного аналізу.

Таблиця 1.3.1. Таблиця дисперсійного аналізу

Джерело варіації	Сума квадратів	Число ступенів вільності	Середній квадрат
Обумовлена регресією
Відносно регресії
Відносно середнього

1.4 -критерій значущості регресії

-критерій. Якщо гіпотезу відхиляти при

(1.4.1)

і не відхиляти в супротивному разі, то з імовірністю гіпотеза відхиляється, коли вона справедлива.

Якщо гіпотеза відхиляється, то регресія значуща, тобто між змінними та існує лінійна залежність.

Якщо ж гіпотеза не відхиляється, то регресія незначуща, між змінними та лінійної залежності немає.

На практиці для перевірки гіпотези також можна використовувати -критерій, який еквівалентний -критерію, оскільки

А

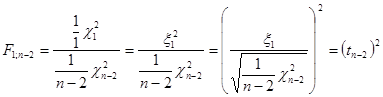
-критерій. Якщо гіпотезу відхиляти при

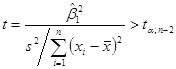(1.4.2)

і не відхиляти в супротивному разі, то з імовірністю гіпотеза відхиляється, коли вона справедлива.

1.5 Геометрична інтерпретація коефіцієнтів регресії

Коефіцієнт визначає точку перетину прямої регресії з віссю ординат, а коефіцієнт характеризує нахил прямої регресії до вісі абсцис.

1

Нехай – кут, утворений прямою регресії з віссю абсцис, тоді

Отже, – це міра залежності від .

Згідно з оцінка показує на скільки змінюється при зміні на одиницю. Знак визначає напрям цієї зміни.