Дипломная работа: Порушення основних припущень лінійного регресійного аналізу

Введемо основні припущення (постулати) про те, що в лінійній моделі

1. Похибка – випадкова величина з середнім і невідомою дисперсією .

2. Похибки некорельовані при , тобто

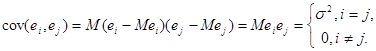
Тому

3. некорельовані при , тобто

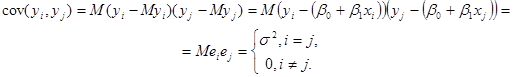
4. Похибка нормально розподілена з параметрами , отже, стають не тільки некорельованими, але й незалежними.

В підрозділі 1.2 за допомогою МНК-метода знайдено оцінку параметра :

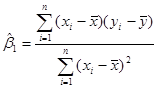
Перепишемо цю оцінку у вигляді

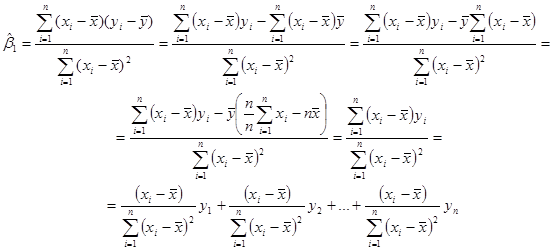
Далі розглянемо функцію

Порахуємо дисперсію цієї функції

,

Якщо – попарно некорельовані (), – константи, крім того, , отже,

У виразі для константи 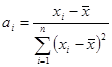, оскільки можна розглядати як величини.

Отже, дисперсія оцінки дорівнює

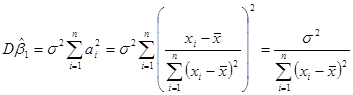(1.6.1)

Стандартне відхилення оцінки – це корінь квадратний з дисперсії

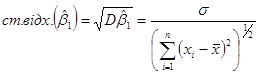(1.6.2)

Оскільки невідома, то заміть неї використовується оцінка , припускаючи, що модель коректна.

Нагадаємо, що середній квадрат дорівнює

Тоді оцінка стандартного відхилення дорівнює

(1.6.3)