Дипломная работа: Порушення основних припущень лінійного регресійного аналізу

Отже, нехай – результати спостережень, які описуються моделлю виду

(1.1.3)

Параметри невідомі, і їх необхідно оцінити за вибіркою .

Для оцінки невідомих параметрів використовують метод максимальної правдоподібності або метод найменших квадратів.

1.2 Метод найменших квадратів

Означення 1.2.1. МНК-оцінкою параметрів будемо називати точку , в якій функція

(1.2.1)

досягає найменшого значення.

Здиференцюємо по , а потім по

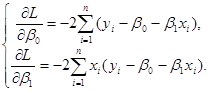
Прирівнюємо похідні нулеві:

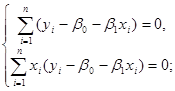
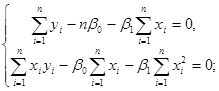
(1.2.2)

(1.2.3)

Останню систему називають системою нормальних рівнянь. Із (1.2.2) маємо:

(1.2.4)

Підставляємо в (1.2.3):

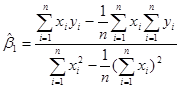(1.2.5)

Оскільки

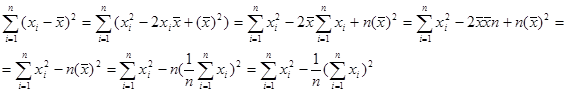
і, крім того,

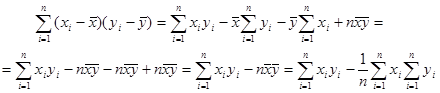
то (1.2.5) запишеться у вигляді

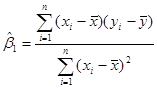
Тоді рівняння простої лінійної регресії має вигляд

Перевіримо, що в точці функція дійсно досягає мінімуму.

Візьмемо другі похідні:

Складаємо дискримінант:

Отже, і . Тоді в точці функція досягає мінімального значення.

Зауваження 1. Якщо в рівнянні регресії