Дипломная работа: Порушення основних припущень лінійного регресійного аналізу
В підрозділі 1.2 було знайдено рівняння простої лінійної регресії:
.
Нехай 
, тоді 
, звідси 
.
А 
, тоді 
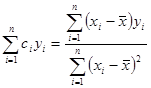, звідси 
.
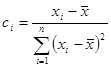Отже,
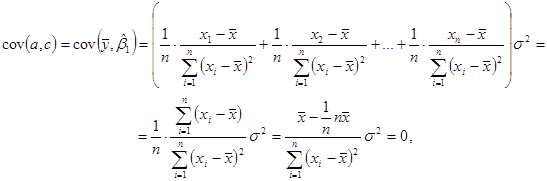
тобто 
і 
некорельовані випадкові величини.
Порахуємо дисперсію 
(або 
при заданому 
).
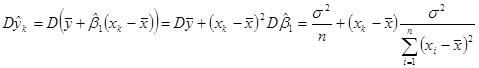(1.8.1)
Стандартне відхилення оцінки при заданому є
(1.8.2)
Оскільки 
невідома, то замість неї використовують оцінку 
, припускаючи, що модель коректна.
Оцінка стандартного відхилення має вигляд:
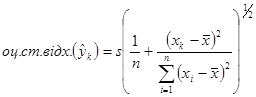(1.8.3)
Ця величина досягає мінімального значення, коли 
, і зростає при віддаленні від 
в будь-якому напрямі.
%-ві довірчі інтервали для регресії мають вигляд:
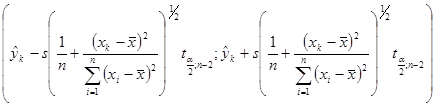
або, що те ж саме,
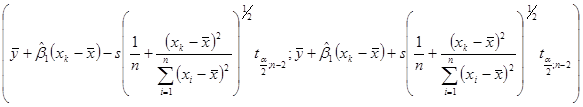Чим більша різниця між та , тим більше відхилення між та (довжина довірчого інтервалу). Останнє означає, що точність прогнозу різна в різних точках .
Дві криві по обидві сторони від лінії регресії визначають 
%-ві довірчі границі й показують, як змінюються границі в залежності від зміни . Ці криві – гіперболи.
Для того, щоб одержати ці криві, необхідно з’єднати неперервною лінією всі значення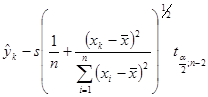 
при всіх 
(нижня гіпербола) та 
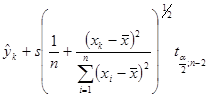при всіх (верхня гіпербола).
1.9 Повторні спостереження. Неадекватність і “чиста” помилка
Побудована лінія регресії – це розрахункова лінія, яка базується на деякій моделі або припущеннях. Але припущення потрібно розглядати як попередні. При деяких обставинах (умовах) можна перевірити, чи коректна (адекватна) побудована модель.
Розглянемо випадок, коли в даних містяться повторні спостереження. Введемо додаткові позначення для множини спостережень при одному й тому ж значенні .
Нехай
– 
спостережень при 
,
– 
спостережень при 
,
. . . . . . . . .
– 
спостережень при 
,
при цьому 
.
Якщо спостереження повторюються (два рази або більше) при однакових значеннях , то ми можемо використати ці повторення для знаходження оцінки для дисперсії . Про таку оцінку говорять, що вона представляє “чисту помилку”, оскільки, якщо однакові, наприклад, для двох спостережень, то тільки випадкові варіації можуть впливати на результати 
і створювати розсіювання між ними. Такі відмінності, як правило, забезпечують одержання надійної оцінки для . Тому при плануванні експериментів має сенс ставити експерименти з повтореннями.
Оцінка величини , пов’язана з “чистою помилкою”, знаходиться так.