Дипломная работа: Простейшие способы обработки опытных данных
Литература . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
Введение.
Данная тема не достаточно широко освещена в математической литературе.В математической статистике при обработке опытных данных чаще всего применяются способ средних и способ наименьших квадратов.
В настоящее время эти способы широко применяются при обработке количественных результатов естественно-научных опытов, технических данных, астрономических и геодезически наблюдений и измерений.
Также возможно применение этих способов при обработке полученных практическим путем данных физических процессов. Например, изучая силу тока в проводниках с постоянным сопротивлением, мы можем зафиксировать значение силы тока при определенном напряжении, то есть не во всех точках, а в небольшом количестве. Применяя способ средних и способ наименьших квадратов, мы имеем возможность с помощью полученных точек подобрать такую функцию, которая бы наиболее близко проходила через эти точки. Это позволяет более полно использовать информацию из наблюдений.
Цели данной работы:
1. Овладение простейшими способами обработки опытных данных.
2. С помощью способа средних и способа наименьших квадратов для экспериментально найденных функционально зависимых величин подобрать функцию, которая наиболее точно описывала бы данный процесс.
3. Применить описанные методы для описания реальных процессов.
§ 1. Простейшие способы обработки опытных данных.
1.1 . Подбор параметров способом средних.
Способ средних основывается на допущении, что наиболее подходящей линией служит та, для которой алгебраическая сумма уклонений равна нулю. Для того чтобы найти этим способом неизвестные постоянные в эмпирической формуле, сначала подставляем в эту формулу все пары наблюдавшихся или замеренных значений xи yи получаем столько уклонений, сколько пар значений (x ; y)в таблице (уклонения—вертикальные расстояния от данных точек до графика функции). Затем распределяем эти уклонения по группам, составляя столько групп, сколько неизвестных параметров эмпирической формулы надо найти. Наконец, приравнивая нулю сумму уклонений по каждой группе, получим систему линейных уравнений относительно параметров.
a) Частный случай.S= A*tq .
| t | t1 | t2 | t3 | t4 | . . . | . . . | tn |
| S | S1 | S2 | S3 | S4 | . . . | . . . | Sn |
Уклонения имеют вид d = A*tq – S. Подставляя значения S и t, взятые из таблицы, и приравнивая уклонения нулю, получим систему уравнений относительно параметров A и q:
![]()
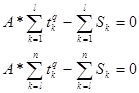 (l<n)
(l<n)
Решение этой системы затруднительно. Поэтому без большей потери в точности, можно приравнять нулю сумму уклонений логарифма S, то есть
d’ = lg A + q * lg T – lg S.
Тогда система примет вид
![]()
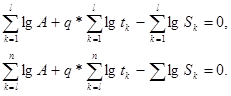 (l<n)
(l<n)
Из системы и определяют q и S.
b) Частныйслучай . S = a0 + a1 *t + a2 *t2 .
| t | t1 | t2 | t3 | t4 | . . . | . . . | tn |
| S | S1 | S2 | S3 | S4 | . . . | . . . | Sn |
Уклонения имеют вид d =a0 + a1 * t + a2 * t2 - S. Подставляя значения S и t, взятые из таблицы, и приравнивая уклонения нулю, получим систему
уравнений относительно параметров a0, a1, a2 :
![]()
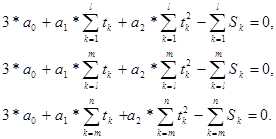 (l<m<n)
(l<m<n)
Из системы и определяют a0, a1, a2 .![]()
1.2 .Подбор параметров способом наименьших квадратов.
На практике часто приходится решать такую задачу. Пусть для двух функционально связанных величин xи yизвестны nпар соответствующих значений ,которые могут быть представлены в виде таблицы
| x | x1 | x2 | x3 | . . . | xn |
| y | y1 | y2 | y3 | . . . | yn |
Требуется в наперед заданной формулеy = f(x,a1 , a2 , …,am )определить mпараметров a1 , a2 , …,am (m < n)так, чтобы в эту формулу наилучшим образом «укладывались» бы известные n пар значений x иy.
Оценки параметров a1 , a2 , …,am определяются из условия, чтобы сумма квадратов отклонений значений y, вычисленных по формуле, от заданных, то есть
L= å [f(xk ,a1 , a2 , …,am ) – yk ] 2
принимала наименьшее значение. Поэтому сам способ получил название способа наименьших квадратов.