Дипломная работа: Расчёт и проектирование замкнутой системы воздушно-динамического рулевого привода летательного
Рис. 1.9 Энергетическая функция привода
Значение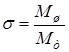 
выбирается из условия обеспечения фазовой частотной характеристики разомкнутого контура, близкой к заданному номинальному значению при возникновении ограничений выходной координаты силовой части привода. При таком значении σ обеспечиваются меньшие фазовые сдвиги, чем при расчёте σ по минимуму расхода, но расход рабочего тела через систему увеличивается, что в случае применения воздушно-динамического привода не является ограничением для проектирования.
Максимальный развиваемый момент определяется по зависимости:
Значение произведения площади поршня на плечо кинематической передачи определяется по зависимости:
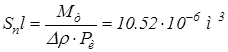
где 
Потребная скорость для обеспечения отработки гармонического сигнала рассчитывается по формуле:
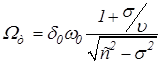
где 
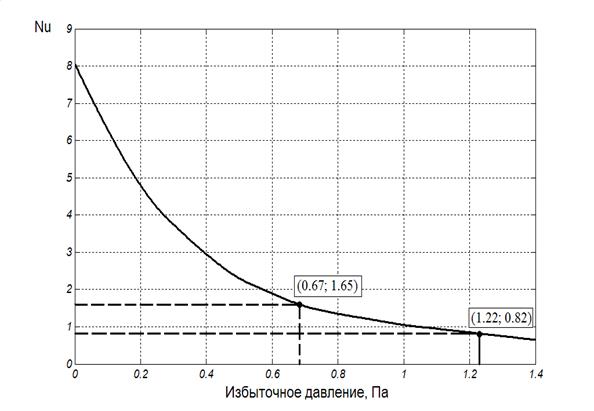
Рис. 1.10 График зависимости числа υ от величины избыточного давления
Структура и параметры автоколебательной системы воздушно-динамического привода определяются для режима наихудших фазовых сдвигов, соответствующего максимуму энергетической функции при нагрузке, имеющей характер перекомпенсации, то есть режима 
(рис. 1.11). Для указанного режима значения параметров следующие:
- число маха М ……………………………………………………..0.894;
- момент шарнирной нагрузки 
………………………..0.265;
- избыточное давление 
………………………………0.667×105 ;
- частота вращения по крену 
……………………………….7.8±2.
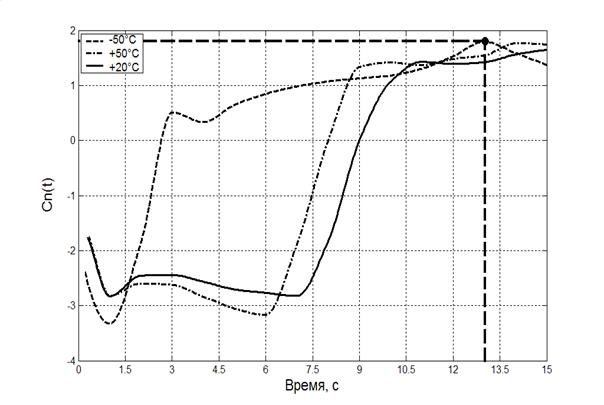
Рис. 1.11 Энергетическая функция привода
Рассчитаем структуру и параметры автоколебательной системы ВДРП на соответствующего режима:
а) рассчитывается допустимая минимальная частота автоколебаний из условия обеспечения разноса рабочей частоты ω0 и частоты автоколебаний ωа :
, где 
б) рассчитывается фазовый сдвиг φn и амплитудная характеристика An исполнительного двигателя на рабочей частоте и частоте автоколебаний.
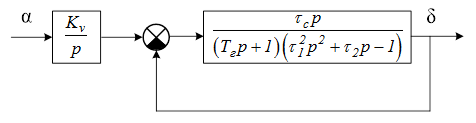
Рис. 1.12 Структурная схема исполнительного двигателя РП
Рассчитаем максимальную скорость на этом режиме, исходя из Ωm на предыдущем: